5

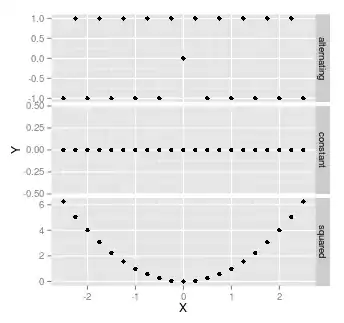
EDIT NOTE: I'm mostly concerned with linear regression with unconstrained y-intercept, but reading about constrained y-intercept, if relevant, is also helpful.

I noticed that for linear regression, the coefficient of determination ($R^2$) can be as high as 1 (if the linear regression fits the given data perfectly). But, can it ever be zero (can there be two variables whose linear $R^2$ is zero)?

I grabbed some random data for dependent variable data (presumably not pseudo-random but ACTUAL random), and I plotted them against an independent variable with the linear regression; you can never really get exactly zero for $R^2$ (so I guess I'm answering my own question). 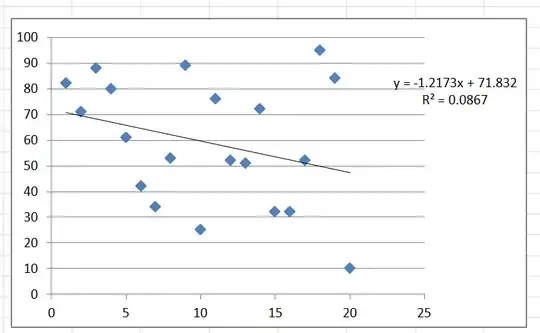random data with non-zero R-squared Why is that? Does this mean that ANY two variables do have SOME linear correlation (no matter how minuscule or small this relation is)?, i.e. can I look at ANY two variables and say that there is SOME linear correlation between them?

So, the matter is NOT whether two variables are linearly correlated, but rather the EXTENT that this linear relationship explains the correlation between the two variables... right? Doesn't this apply to all other regression models (non-linear)?

Ferdi
  • 4,882
  • 7
  • 42
  • 62
Cashew
  • 153
  • 1
  • 6
  • 2
    Does this help? http://stats.stackexchange.com/questions/12900/when-is-r-squared-negative – Jack Tanner Nov 29 '12 at 05:05
  • well, it does shed some light on the topic (now I realize that my question only concerns linear regression where the y-intercept is not constrained)... – Cashew Nov 29 '12 at 05:14

2 Answers2

13

Yes, when ever there is no linear relationship between variables. For example, when either X or Y are constant, or where each high-low data points are balanced by high-high, or low-low data points. For example, $X=(1,1,2,2)$, $Y=(1,2,1,2)$, or $X=(-2,1,0,1,2)$, $Y=X^2$

Here are some examples: all of these have correlation of 0, and hence a coefficient of determination of zero:

No correlation graphs

It's worth noting that as soon as there's any randomness, then there's almost certainly going to be some correlation. With a small sample size, that correlation might be quite high - wouldn't be unusual to have a correlation as high as $\pm$0.3, with a sample size of 20.

naught101
  • 4,973
  • 1
  • 51
  • 85
  • Wow. That is a facepalm moment for me (because now I remember seeing this before [flashback deja vu at me asking this before and getting same answer]). Oh, well. Thanks anyways! – Cashew Nov 29 '12 at 06:04
  • 1
    @Bash, everyone has them :) added some notes about randomness – naught101 Nov 29 '12 at 06:14
  • 4
    One additional note - that "randomness" could come from pure measurement error. In the real world, nothing gets measured perfectly, so there will always be some correlation. – Peter Flom Nov 29 '12 at 11:44
  • @PeterFlom that's exactly what I was thinking. So the answer to my question is: in the real world, no. Theoretically, yes... right? – Cashew Nov 29 '12 at 18:50
  • 1
    @Bash Yes, exactly – Peter Flom Nov 29 '12 at 19:51
4

The null hypothesis is always false, basically. That's why people shouldn't just report p values (to make up a stupid example, in the UK highly significant correlation between house number and income: sample size of 20 million, r=0.004, p<.0001).

Chris Beeley
  • 5,465
  • 5
  • 36
  • 40
  • great insight. I will need to look into why the null hypothesis is always false, though. thanks! – Cashew Nov 30 '12 at 16:06
  • @Bash: Because any randomness present will lead to *some* correlation, and the null hypothesis is no effect, or zero correlation. – naught101 Dec 01 '12 at 03:09
  • I'd go a little further and say that whenever you conduct a study looking at the association between two variables, if you think there might possibly be an association, there will always be a tiny effect. So a study correlating number of whales in the ocean with the winner of the Superbowl will find random noise which invalidates the null hypothesis. But a sensible study (do men or women have faster reactions times, are French people better than Germans at remembering lists of numbers) will always find a real effect, that may be tiny. So tiny, in fact, that it is not worth bothering about – Chris Beeley Dec 11 '12 at 13:28