statistical significance for non linear data

Question

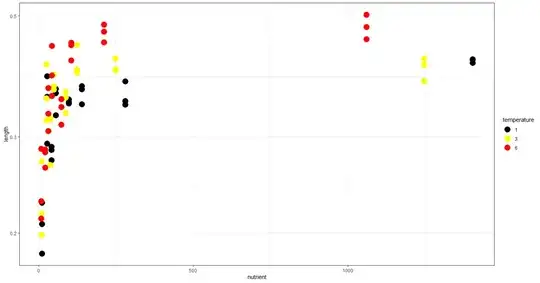
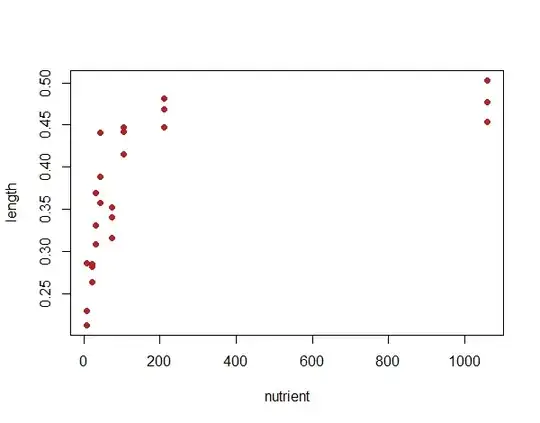
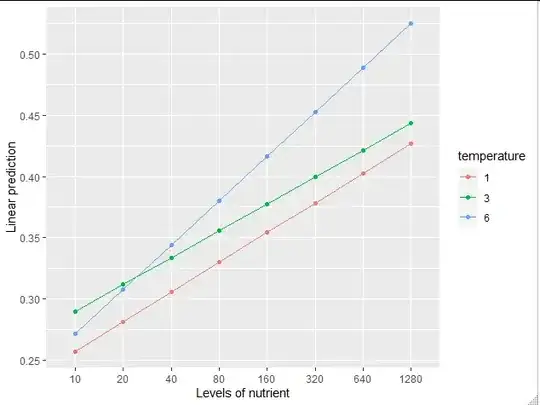
I have a data-set with two independent (continuous) variables: temperature (1, 3, 6 degrees) and nutrient concentration (~ 9-1400) and one dependent variable (length), with replicates (three independent replicates at each condition). I'd like to analyze the interactive effects of nutrients and temperature on size.

When I plot the data, it is clear (visually) that length increases with nutrient concentration (to a point), and temperature doesn't play a big rule in influencing length.

However, I would like to use some statistical test to back up my observations.

require(lme4) 
require(nlme)
require(lmerTest)
require(gam)

#this is the data I have
temperature <- c(1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6)

nutrient <- c(41.922282,41.922282,41.922282,37.23794,37.23794,37.23794,31.662541,31.662541,31.662541,279.720746,279.720746,279.720746,248.465109,248.465109,248.465109,211.264016,211.264016,211.264016,27.946784,27.946784,27.946784,24.824046,24.824046,24.824046,21.1073,21.1073,21.1073,55.899183,55.899183,55.899183,49.65308,49.65308,49.65308,42.218842,42.218842,42.218842,97.838316,97.838316,97.838316,86.905988,86.905988,86.905988,73.89411,73.89411,73.89411,10.479381,10.479381,10.479381,9.308428,9.308428,9.308428,7.914737,7.914737,7.914737,1404.251692,1404.251692,1404.251692,1247.342413,1247.342413,1247.342413,1060.585803,1060.585803,1060.585803,139.790093,139.790093,139.790093,124.170127,124.170127,124.170127,105.578928,105.578928,105.578928)

replicate <- c("1C_41.922282","1C_41.922282","1C_41.922282","3C_37.23794","3C_37.23794","3C_37.23794","6C_31.662541","6C_31.662541","6C_31.662541","1C_279.720746","1C_279.720746","1C_279.720746","3C_248.465109","3C_248.465109","3C_248.465109","6C_211.264016","6C_211.264016","6C_211.264016","1C_27.946784","1C_27.946784","1C_27.946784","3C_24.824046","3C_24.824046","3C_24.824046","6C_21.1073","6C_21.1073","6C_21.1073","1C_55.899183","1C_55.899183","1C_55.899183","3C_49.65308","3C_49.65308","3C_49.65308","6C_42.218842","6C_42.218842","6C_42.218842","1C_97.838316","1C_97.838316","1C_97.838316","3C_86.905988","3C_86.905988","3C_86.905988","6C_73.89411","6C_73.89411","6C_73.89411","1C_10.479381","1C_10.479381","1C_10.479381","3C_9.308428","3C_9.308428","3C_9.308428","6C_7.914737","6C_7.914737","6C_7.914737","1C_1404.251692","1C_1404.251692","1C_1404.251692","3C_1247.342413","3C_1247.342413","3C_1247.342413","6C_1060.585803","6C_1060.585803","6C_1060.585803","1C_139.790093","1C_139.790093","1C_139.790093","3C_124.170127","3C_124.170127","3C_124.170127","6C_105.578928","6C_105.578928","6C_105.578928")

length <- c(0.284222,0.271812,0.287842,0.266703,0.325212,0.323167,0.368914,0.307848,0.331279,0.349361,0.344158,0.379752,0.418207,0.398789,0.397851,0.481935,0.46838,0.447341,0.291471,0.38784,0.355353,0.353436,0.40762,0.321866,0.284687,0.26343,0.281308,0.361157,0.367518,0.328645,0.390822,0.372086,0.366396,0.357013,0.388808,0.440506,0.351289,0.348172,0.345575,0.35433,0.363403,0.332073,0.34037,0.315966,0.351829,0.207838,0.227385,0.183385,0.198436,0.217075,0.270751,0.28564,0.228815,0.212524,0.410496,0.415918,0.416817,0.406967,0.38017,0.417732,0.453175,0.502706,0.477136,0.371708,0.344421,0.366723,0.398991,0.393513,0.442445,0.414689,0.442346,0.446943)

mydata <-data.frame(nutrient, temperature, replicate, length)

#to keep things simple, I am using a linear mixed effects model, and using my "replicates" as random effects. 
#I also try different transformations to handle the non-linearity in my data

linear <- lmer (length ~ nutrient*temperature +(1|replicate),  data= mydata)
log <- lmer (length ~ log(nutrient)*temperature +(1|replicate),  data= mydata)
sqrt <- lmer (length ~ sqrt(nutrient)*temperature +(1|replicate),  data= mydata)

#then I do an AIC test to see which of these linear transformations is best 

AIC(linear, log, sqrt)

#this shows that the log transformation is the best model. 

Then I take the log model, and run it with nutrient alone, temperature alone, nutrient*temperature, and nutrient+temperature effects: 

log_interactive <- lmer (length ~ log(nutrient)*temperature +(1|replicate),  data= mydata)
log_additive <- lmer(length ~ log(nutrient)+temperature +(1|replicate),  data= mydata)
log_temperature <- lmer (length ~ temperature +(1|replicate),  data= mydata)
log_nutrient <- lmer (length ~ log(nutrient) +(1|replicate),  data= mydata)

AIC(log_interactive, log_additive, log_temperature, log_nutrient)
#this shows that the best model is the nutrient alone one. 

My interpretation of this is that nutrients play a role in influencing size, temperature does not influence size, and there is no temperature-nutrient interaction in influencing size.

I have a very weak statistical background and I am not sure that this is the correct approach to take to analyze this data and generate p-values for the different effects. Any help would be appreciated. Would it be better to do non-linear statistics on this ?

Thanks in advance!

Answer 1

Often with data that look like this, the goal is to determine the x value beyond which there is no further (statistical) increase in the y variable. And also to determine the plateau y value. This might be done with linear-plateau or quadratic-plateau models. But eyeballing your data, a Cate-Nelson approach might be more useful to determine these values. This approach basically separates the low-x-low-y values from the high-x-high-y values.

As a first approach, I might look at the data for each temperature separately. I might estimate the critical x value and plateau value for each of these separately, and then determine if the temperatures have a statistical effect by comparing the 95% confidence intervals of these statistics. It looks to me that Temperature 6 has a higher plateau than Temperature 1.

For the purposes of this answer, I'm just going to examine the data for Temperature 6.

---

First, let's try a linear plateau model on the Temperature 6 data.

temperature <- c(1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6,1,1,1,3,3,3,6,6,6)

nutrient <- c(41.922282,41.922282,41.922282,37.23794,37.23794,37.23794,31.662541,31.662541,31.662541,279.720746,279.720746,279.720746,248.465109,248.465109,248.465109,211.264016,211.264016,211.264016,27.946784,27.946784,27.946784,24.824046,24.824046,24.824046,21.1073,21.1073,21.1073,55.899183,55.899183,55.899183,49.65308,49.65308,49.65308,42.218842,42.218842,42.218842,97.838316,97.838316,97.838316,86.905988,86.905988,86.905988,73.89411,73.89411,73.89411,10.479381,10.479381,10.479381,9.308428,9.308428,9.308428,7.914737,7.914737,7.914737,1404.251692,1404.251692,1404.251692,1247.342413,1247.342413,1247.342413,1060.585803,1060.585803,1060.585803,139.790093,139.790093,139.790093,124.170127,124.170127,124.170127,105.578928,105.578928,105.578928)

replicate <- c("1C_41.922282","1C_41.922282","1C_41.922282","3C_37.23794","3C_37.23794","3C_37.23794","6C_31.662541","6C_31.662541","6C_31.662541","1C_279.720746","1C_279.720746","1C_279.720746","3C_248.465109","3C_248.465109","3C_248.465109","6C_211.264016","6C_211.264016","6C_211.264016","1C_27.946784","1C_27.946784","1C_27.946784","3C_24.824046","3C_24.824046","3C_24.824046","6C_21.1073","6C_21.1073","6C_21.1073","1C_55.899183","1C_55.899183","1C_55.899183","3C_49.65308","3C_49.65308","3C_49.65308","6C_42.218842","6C_42.218842","6C_42.218842","1C_97.838316","1C_97.838316","1C_97.838316","3C_86.905988","3C_86.905988","3C_86.905988","6C_73.89411","6C_73.89411","6C_73.89411","1C_10.479381","1C_10.479381","1C_10.479381","3C_9.308428","3C_9.308428","3C_9.308428","6C_7.914737","6C_7.914737","6C_7.914737","1C_1404.251692","1C_1404.251692","1C_1404.251692","3C_1247.342413","3C_1247.342413","3C_1247.342413","6C_1060.585803","6C_1060.585803","6C_1060.585803","1C_139.790093","1C_139.790093","1C_139.790093","3C_124.170127","3C_124.170127","3C_124.170127","6C_105.578928","6C_105.578928","6C_105.578928")

length <- c(0.284222,0.271812,0.287842,0.266703,0.325212,0.323167,0.368914,0.307848,0.331279,0.349361,0.344158,0.379752,0.418207,0.398789,0.397851,0.481935,0.46838,0.447341,0.291471,0.38784,0.355353,0.353436,0.40762,0.321866,0.284687,0.26343,0.281308,0.361157,0.367518,0.328645,0.390822,0.372086,0.366396,0.357013,0.388808,0.440506,0.351289,0.348172,0.345575,0.35433,0.363403,0.332073,0.34037,0.315966,0.351829,0.207838,0.227385,0.183385,0.198436,0.217075,0.270751,0.28564,0.228815,0.212524,0.410496,0.415918,0.416817,0.406967,0.38017,0.417732,0.453175,0.502706,0.477136,0.371708,0.344421,0.366723,0.398991,0.393513,0.442445,0.414689,0.442346,0.446943)

mydata <-data.frame(nutrient, temperature, replicate, length)

T6 = mydata[mydata$temperature==6,]

plot(length ~ nutrient, data=T6, pch=16, col="firebrick")

###  Guess some reasonable initial values for parameters

a.ini     = 0
b.ini     = 1000
clx.ini   = 200

###  Define linear plateau function

linplat = function(x, a, b, clx)
          {ifelse(x < clx, a + b * x,
                           a + b * clx)}

###  Find best fit parameters

model = nls(length ~ linplat(nutrient, a, b, clx),
            data = T6,
            start = list(a   = a.ini,
                         b   = b.ini,
                         clx = clx.ini),
             trace = FALSE,
             nls.control(maxiter = 1000))

summary(model)

   ### Parameters:
   ###      Estimate Std. Error t value Pr(>|t|)    
   ### a   2.607e-01  1.711e-02  15.231 8.01e-13 ***
   ### b   1.618e-03  2.972e-04   5.446 2.11e-05 ***
   ### clx 1.305e+02  1.957e+01   6.665 1.35e-06 ***

plateau = 2.607e-01 + 1.618e-03 * 1.305e+02
plateau

   ### 0.472

So the critical x value is about 130 and the plateau is 0.472. This suggests that above a nutrient value of 130, there is no further rise in length with increasing nutrient value (for the Temperature 6 data).

With the caveat that I am the author of the page, additional code to determine confidence intervals for the parameters, p value for the overall model, and pseudo r-square for the model can be found at rcompanion.org/handbook/I_11.html.

This model is easy enough to plot, but I'll use a convenience function from the rcompanion package.

require(rcompanion)

plotPredy(data  = T6,
          x     = nutrient,
          y     = length,
          model = model,
          xlab  = "Nutrient",
          ylab  = "Length for T 6")

This model might be okay for these data. But in my mind, the data below nutrient = 200 don't really support a linear rise in length in relation to nutrient. The residuals also reveal that the model doesn't quite fit the trend of the data in this region.

plot(predict(model), residuals(model))

hist(residuals(model), col="darkgray")

We could try a quadratic-plateau model. As it turns out, it's not much different.

Another idea is to use a Cate-Nelson approach. The goal here is to find a critical x value and a critical y that separates the low-x-low-y values from the high-x-high-y values. There are statistical approaches that can be employed. But if there are cutoff values of x or y that may be meaningful, this analysis can be accomplished by simply eyeballing these values. (An example might be, we are interested in getting at least 85% of maximum yield of our crop, so we want to determine the nutrient level in the soil (x) that gives us (usually) at least 85% of maximum yield (y).)

I won't get into the specifics of analysis, but there are some resources here: rcompanion.org/rcompanion/h_02.html, (with the caveat that I am the author of that page).

The following plots one possible solution.

[Note the points in this plot are slightly jittered from the original data.]

It turns out that this solution perfectly separates the data. That is, all data points fall into Quadrants II and IV.

The Critical x value is 158, and the Critical y is 0.447. That is a nutrient value greater than 158 is likely to yield a length of greater than 0.447. And vice-versa.

sum((T6$nutrient < 158) & (T6$length < 0.447142))

   ### 18

sum((T6$nutrient > 158) & (T6$length > 0.447142))

   ### 6

sum((T6$nutrient < 158) & (T6$length > 0.447142))

   ### 0

sum((T6$nutrient > 158) & (T6$length < 0.447142))

   ### 0

Answer 2

If you do as was suggested in a comment by Michael Lew and use log(nutrient) in the plot, you see a reasonably linear trend for each temperature:

lattice::xyplot(length ~ log(nutrient) | temperature, data = mydata)

Accordingly, I tried the following model, which fits quite well:

mylm = lm(length ~ factor(temperature) * log(nutrient), data = mydata)

The fitted trends can be visualized as follows:

library(emmeans)
emmip(mylm, temperature ~ nutrient, at = list(nutrient = c(10,20,40,80,160,320,640,1280)))

This appears as linear trends because the values I chose go up exponentially. If we look at the same plot with a linear scale...

 pdat = .Last.value$data
lattice::xyplot(yvar ~ nutrient, groups = ~temperature, data = pdat, type="l")

You can compare the slopes of the lines in the preceding plot as follows:

> emtrends(mylm, pairwise ~ temperature, var = "log(nutrient)")
$emtrends
 temperature log(nutrient).trend      SE df lower.CL upper.CL
           1              0.0350 0.00614 66   0.0228   0.0473
           3              0.0317 0.00614 66   0.0194   0.0439
           6              0.0523 0.00614 66   0.0400   0.0645

Confidence level used: 0.95 

$contrasts
 contrast estimate      SE df t.ratio p.value
 1 - 3     0.00333 0.00868 66  0.383  0.9223 
 1 - 6    -0.01728 0.00868 66 -1.992  0.1222 
 3 - 6    -0.02061 0.00868 66 -2.375  0.0527 

P value adjustment: tukey method for comparing a family of 3 estimates

I think this model fits the data better than broken lines or polynomials. It is parsimonious, and the interpretation is simple.

Answer 3

The first step usually taken for non-linear relationships like this is by adding a polynomial term. A linear relationship is y ~ x, but you can use a quadratic approximation by doing y ~ x + x ^ 2. This is like x interacting with itself: the relationship between x and y depends on the value of x. It is still a linear model, since you are adding up coefficients, but it is a very common "trick" to approximate nonlinear relationships while still using all of the benefits of the linear model.

Here's code how to do it with lme4 and then the plotted relationship:

library(lme4) 
library(lmerTest)

# linear nutrient and temperature main effects
# treating temperature as numeric
m1 <- lmer(length ~ nutrient + temperature + (1 | replicate), mydata)
summary(m1) # significant main effects of nutrient, but not temeprature

# looks like curvilinear relationship between nutrient and length
# simplest way to do this is quadratic: x + x ^ 2
# you can think of x ^ 2 as "x times x" or an interaction between x and itself
# poly() gives us polynomial, and we indicate 2 for squared
m2 <- lmer(length ~ poly(nutrient, 2) + temperature + (1 | replicate), mydata)
summary(m2) # significant quadratic relationship

# does this quadratic relationship depend on temperature?
m3 <- lmer(length ~ poly(nutrient, 2) * temperature + (1 | replicate), mydata)
summary(m3)
# yes, p = .033. we see the quadratic effect of nutrient and
#   linear of temperature depend on one another. what does this look like? 
#   let's get predicted values for the data and plot it

library(ggplot2)
library(emmeans)
pred <- emmeans(
  m3, # specify model 
  c("nutrient", "temperature"), # specify predictors
  # specify at what points you want to get predictions:
  at = list(
    nutrient = seq(8, 1000, length.out = 20),
    temperature = c(1, 3, 6)
  )
)

# make data frame for plotting
pred <- as.data.frame(pred)

# and plot
ggplot(pred, aes(x = nutrient, y = emmean, 
                 group = factor(temperature),color = factor(temperature))) +
  geom_line() +
  labs(y = "predicted length")

m3 has the quadratic relationship between nutrient and length that depends on temperature, and you can see that coefficient is significant. Just the fixed effect coefficient table from summary(m3):

Fixed effects:
                                Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)                     0.333554   0.017941 17.999958  18.591 3.39e-13 ***
poly(nutrient, 2)1              0.472626   0.162941 17.999958   2.901  0.00953 ** 
poly(nutrient, 2)2             -0.077723   0.150528 17.999958  -0.516  0.61190    
temperature                     0.004344   0.004663 17.999958   0.932  0.36386    
poly(nutrient, 2)1:temperature -0.103052   0.053974 17.999958  -1.909  0.07230 .  
poly(nutrient, 2)2:temperature -0.109066   0.047116 17.999958  -2.315  0.03263 *  

And here's what the call to ggplot returns:

If you are interested in what the different predicted effects for replicate look like, you could also add (1 + replicate) to the call to emmeans and include the IDs that you want to look at.