Rationale for elliptical region of correlations in gene expression data

Question

I am analysing an RNA seq data set and I am trying to look at correlation between expression values of significant genes in 4 different biological duplicates and their clinical parameters.

Here, I calculate the correlation coefficient between mfOXP3 level and my 250 significant genes and between hFOXP3 level and these same 250 significant genes. Then I plot the coefficients of mFOXp3 and against the coefficient of hFOXP3 And I have this plot - an elliptical shape... (see below)

I tried with different other parameters and I found different shapes, but always with kind of elliptical shape.

Answer 1

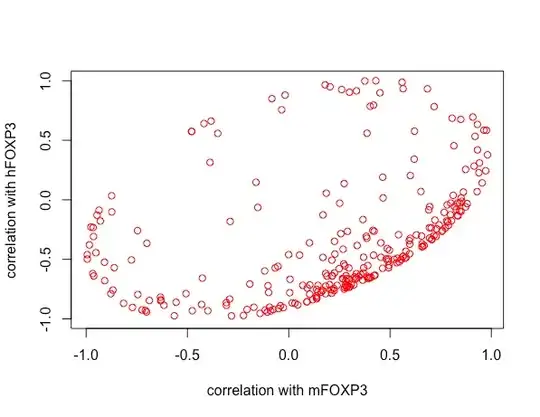
That the points all lie within an ellipse is a mathematical restriction: it does not otherwise reveal anything about your data.

Generally, when you have two random variables (or data vectors) $Y$ and $Z$ with a correlation $\rho$ between them, the correlations between a third variable $X$ and these two are restricted. Writing these correlations as $\rho_1$ and $\rho_2,$ the correlation matrix for $(X,Y,Z)$ is

$$\pmatrix{1 & \rho_1 & \rho_2 \\ \rho_1 & 1 & \rho \\ \rho_2 & \rho & 1}.$$

You have plotted the $(\rho_1,\rho_2)$ points for $250$ data vectors $X.$ (I think that's an interesting idea.)

Because correlations are the covariances between the standardized versions of those variables, and covariances are variances, and variances are the expectations of squared numbers, all correlation matrices must be positive semidefinite. Sylvester's Criterion gives a way to check this property. In this case it says we need to verify that $1-\rho^2 \ge 0$ and that the determinant of the entire matrix is non-negative. The first is obvious and the second, after some easy algebra, comes down to the relation

$$ \{(\rho_1,\rho_2) \mid \rho_1^2 + \rho_2^2 - 2\rho\, \rho_1\rho_2\ \le\ 1-\rho^2\}$$

describing a subset of the $(\rho_1,\rho_2)$ plane.

This is recognizable as the equation of a symmetric ellipse and the inequality specifies the points inside it. Moreover, you can check that the points

$$(1, \rho),\quad (\rho, 1), \quad(-\rho, -1), \quad(-1,-\rho)$$

all satisfy this constraint. Since they intersect the boundary of the square $[-1,1]\times[-1,1],$ we see that this ellipse is inscribed in the square. This ellipse appears in the illustrations at https://stats.stackexchange.com/a/71303/919, which discusses them in much more detail.

Finally, the distribution of the points within the ellipse may be of some interest--but interpreting that distribution is not easy, given how indirectly this information reflects on the relationships among your variables. Any association among correlations (which are functions of second trivariate moments) already reflects some kind of fourth order moments of the data. Finding a visualization a little less remote from the data may be more insightful.

Answer 2

Basically, there is a correlation among your correlations due to a) spontaneous correlation between mFOXP3 and hFOXP3 and b) using the partial correlations for the multivariate model of $$\text{GENE} = \alpha + \beta_1 +\text {hFOXP3 } + \beta_2 \text{mFOXP3 } + \epsilon.$$ The part that's missing from the axis labels is correlation with what if we put "with $X$" on the x-axis and y-axis label it's immediately clear that it's an artifact of using the same residuals of a particular gene for a replicate as well as the endogenous correlation between mFOXP3 and hFOXP3. The fact that both ellipses are strongly centered on 0 means that we don't have any strong evidence of correlation between m- and h- FOXP3 nor with the genes in the data: and that the region is induced by random variation.

We see similar elliptical regions when we plot multivariate regression coefficients. Sometimes a hypothesis test is simultaneously that $\beta_1 = \beta_2 = 0$ such as giving a stronger test of significance in a linear regression by including linear and quadratic terms: i.e. for the null to be true, BOTH have to be 0.

Answer 3

Consider what you're not seeing - there consistently are no points strongly anticorrelated with mFOXP3 but strongly correlated with hFOXP3.

Considering those two are variations on a theme for one underlying function and thus somewhat common structure, it would be surprising if their association with the expression of any gene was strong in opposite directions.

You see some points where the correlation weakened or was lost, which makes sense - loss-of-function mutations are reasonably common when a receptor stops recepting, sometimes you get change-of-function, but it would be astonishingly unlikely if a change in structure flips the biological effect on its head directly, rather than just by jamming up the gears.