I read the following: 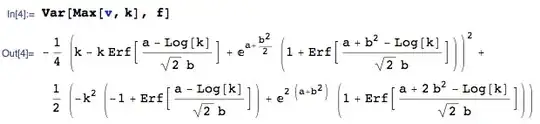 in John Fox's Applied Regression Analysis and Generalized Linear Models.
in John Fox's Applied Regression Analysis and Generalized Linear Models.
I don't understand this distinction.
In OLS, I have
$$E[y_i|X] = E[x_i^T\beta + \epsilon_i|X] = x_i^T\beta + E[\epsilon_i |X]= x_i^T\beta$$ Now suppose I have a log-linear model
$$\log(y) = X\beta + \epsilon$$
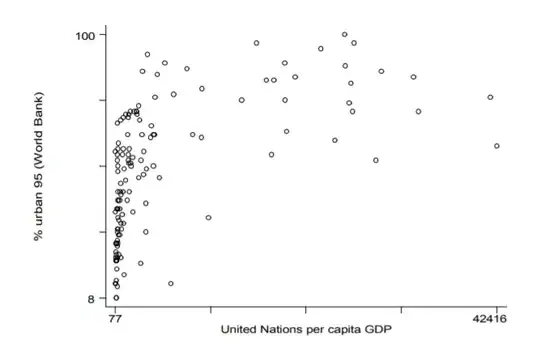
where transforming the data is similar to this case
where transforming the data leads to a linear relationship. source: https://kenbenoit.net/assets/courses/ME104/logmodels2.pdf
What do GLMs do that is different from this?