3

What does the most ideal power curve look like?

What does the worst power curve look like?

Does there exist good power curves or bad power curves?

Obviously there exists more powerful and less powerful hypothesis tests. I'm not sure whether looking at their power curves is useful for ranking their power.

Example of power curve

enter image description here

1 Answers1

7

I recognize that image!

[Since that hint was apparently overly subtle, you should - in accordance with the stackexchange rules - credit the person who created it and link to where you got it from. Since it was originally posted here on stackexchange, it should not be too difficult to figure out who to credit.]

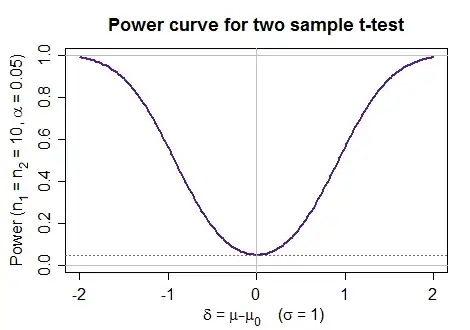
High power is better whenever the null is false, so at a fixed significance level, the steeper the curve rises toward 1 (where it would always reject), the better, and the shallower, the worse it is (the more often you fail to reject when you should).

Here's a sequence of power curves for a two tailed symmetric test, like a two-tailed t-test, say.

sequence of increasingly steep power curves

The flatter curves (which are red-orange in the plot, apart from the totally flat one in grey) are relatively poor -- power is comparatively low while the steeper (bluer) ones are relatively good - power jumps up very near 1 as soon as the difference moves a little distance from the null value.

For a one tailed test you want the rejection rate to not exceed the significance level on the part where the alternative doesn't hold (rejection rate $\leq \alpha$) and then on the part where the alternative does hold, for it to rise as rapidly as possible toward 1.

Ideally, in whichever case, you reject when the null is false, so you would like power to be at 1 everywhere the null is false. This is usually not attainable in practice.

For some situations, there may be a uniformly most powerful test; in particular you might like to read about the Karlin-Rubin theorem. In such a case, for a given set of assumptions and sample size there may be a "best" power curve you can attain under those assumptions across a sequence of alternatives (though you can do better by increasing the sample size).

Even when there isn't a single "best" test, you can compare different tests under some particular sequence of alternatives.

For example, there's plots showing some comparisons of different tests in specific situations (both in question and answer) in this question How to graph Wilcoxon test power R

It is sometimes the case that a power curve dips below the significance level when the alternative is true; in particular this is the case with some omnibus-alternative tests (like goodness of fit tests). Such tests are said to be biased.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Given the image, Would the most ideal power curve be a flat line at power=1? For all deltas, the power is 1? –  Jan 22 '20 at 01:50
  • 1
    For all values of the parameter except those specified under the null (always reject the null when it's false is ideal, naturally). However power curves are normally continuous so you can't get there. Hang on and I'll draw some pictures. – Glen_b Jan 22 '20 at 01:52
  • Does a hypothetical super steep power curve actually correspond to any known hypothesis test or is it a theoretical limit? Do any known hypothesis test have a super flat power curve? I heard non-parametric tests have less power than parametric ones. –  Jan 22 '20 at 02:15
  • Is it possible to generate power curves for score-tests, wald-test, LR test? –  Jan 22 '20 at 02:18
  • Does a uniformly most powerful test have a power curve graphical interpretation? Does UMP tests power curve look different from non-uniformly most powerful tests? –  Jan 22 '20 at 02:21
  • What does asymptotic power look like on a power curve? –  Jan 22 '20 at 02:23
  • An answer is not an invitation to machine-gun a series of completely new questions. If the answer to the question that was asked is unclear, comments are a good way to seek clarification, and maybe add a small additional detail. Note however, that "Are steeper power curves also better even for non-symmetric hypothesis test or one-tailed tests?" is already covered by my first comment. For some of the rest of it a new question or questions may be in order. I will add some small clarifications. – Glen_b Jan 22 '20 at 02:25
  • 1
    Nonparametric tests are NOT less powerful in general. *Some* nonparametric tests are less powerful than the most powerful parametric test in *exactly the situation where the parametric test is most powerful*. But even then there's often a nonparametric test that - at the attainable significance levels of the parametric test - may be equally powerful, or very nearly so. As an example, take the t-test; if all its assumptions hold, it's hard to beat (but you can do as well, with a judicious choice of test), and if you modify the situation just a little, you can beat it with a nonparametric test. – Glen_b Jan 22 '20 at 02:35
  • For example, if you follow the link near the bottom of my answer you'll see an example in the question where both the signed rank test and the sign test have better power than a parametric test (the one-sample t-test) - specifically in that case, because the population distribution is not normal but t-distributed with low degrees of freedom, so the tails are heavy (none of them is the most powerful test possible for this situation). Under different assumptions, each of the three tests will beat the other two. – Glen_b Jan 22 '20 at 02:56
  • I'm curious: where do you recognize that image from? – Cliff AB Feb 27 '20 at 18:35
  • 1
    It's an image I made in R. For example, I used it [here](https://stats.stackexchange.com/a/118528/805) – Glen_b Feb 27 '20 at 21:49
  • 1
    Also [here](https://stats.stackexchange.com/a/283935/805). OP presumably grabbed it from one of my posts (which is fine), but didn't credit me as the source (which contravenes both the creative commons license terms and the stackexchange rules; unfortunately my comment wasn't enough of a prompt). – Glen_b Feb 27 '20 at 22:13
  • That's an interesting usage of CV I hadn't thought of: when preparing slides, I'm constantly reproducing what should be stock statistical images (i.e., a Gaussian Process conditional on a small number of points), but I'm not sure about licenses from Google Images searches. I should just be looking at CV and citing it! – Cliff AB Feb 28 '20 at 18:02
  • Yes, if you can find what you need here, the licensing rules are pretty simple and not onerous (once you figure out the details, to my recollection a short bit of text plus a link satisfy both the license requirements and the stackechange rules). My own images tend to be fairly low-res but may still be okay for a slide. Further, many posts give explicit code, so you can always generate your own image in those cases (though crediting the source of the code would be a natural thing to do) – Glen_b Feb 29 '20 at 02:20
  • It's also easy to generate a citation for a whole post (question or answer) automatically from the link at the bottom of the post. – Glen_b Sep 08 '21 at 04:02