Is there a simpler probabilistic causal model that describes this data generating process?

Question

Consider the following data generating process:

1. A person with gender male or female is selected from a population with probability $\alpha$ of selecting female.
2. The person is offered a drug to treat an illness.
3. If the person is male, he decides to take the drug with probability $\beta$. If the person is female, she decides to take the drug with probability $\gamma$.

Below I specify what I believe is a faithful probabilistic causal model (PCM) for this process, I'd like to know if there is a simpler one. In particular:

Is there a PCM that faithfully represents the data generating process above but with fewer exogenous variables?

I don't think there is, but for some reason, I feel like the model below is needlessly complex.

---

Let $U_G$, $U_M$, and $U_F$ be random variables with values in $\{0,1\}$ such that

\begin{align} U_G \sim \mathrm{Bernoulli}(\alpha), \qquad U_M \sim \mathrm{Bernoulli}(\beta), \qquad U_F \sim \mathrm{Bernoulli}(\gamma). \end{align}

Let functions $f_G$ and $f_D$ be defined as follows:

\begin{align} f_G(u_G) = u_G, \qquad f_D(g, u_F, u_M) = gu_F + (1-g)u_M, \end{align}

and define the random variables $G$ and $D$ as

\begin{align} G = f_G(U_G), \qquad D = f_D(G, U_F, U_M). \end{align}

Finally let $U = \{U_G, U_M, U_F\}$, $V = \{G, D\}$, $F = \{f_G, f_D\}$, and $P$ be the probability distribution over $U$ specified above via independent Bernoulli distributions, then $(U, V, F, P)$ is a PCM, and I believe it faithfully represents the process describes above.

---

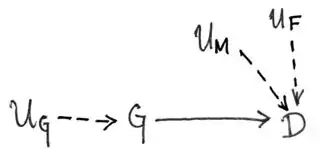
The corresponding causal graph is:

The idea here is that the exogenous variable $U_G$ captures the randomness inherent in selecting gender $G$ as either male or female with value $G = 1$ corresponding to female and value $G = 0$ corresponding to male. The exogenous variables $U_F$ and $U_M$ capture the gender-dependent randomness in whether a person will or will not take the drug with $D = 1$ corresponding to taking the drug and $D = 0$ corresponding to not taking the drug. The function $f_D$ is constructed to ensure that if the person selected turns out to be female, the probability of taking the drug follows the distribution of $U_M$ while if the person selected turns out to be make, the probability of taking the drug follows the distribution of $U_F$.

Answer 1

Is there a PCM that faithfully represents the data generating process above but with fewer exogenous variables?

I am not sure I understand what you want, but if the goal is just to reduce the number of exogenous variables, you can define just one exogenous random variable $U_{D}$, instead of the two you currently have $U_{M}$ and $U_{F}$.

Let $U_D$ and $U_{g}$ be uniformly distributed over (0,1). You can write structural equations for your model in the form of,

$$ G = I(U_{G} > \alpha)\\ D = G\times I(U_{D} > \gamma) + (1-G)\times I(U_{D} > \beta) $$

Where $I(\cdot)$ is the indicator function.

Answer 2

I think there should be only two random variables $G$ and $D$. $G$ maps into the set $\{M, F\}$ and $D$ maps into the set $\{0,1\}$ (0=patient did not take the drug, 1=patient took the drug). Then we define/assume ($p$ always represents densities, i.e. since all the variables are discrete, $p(d) = P[D=d], p(d,g) = P[D=d ~\text{and}~ G=g]$ and so forth)

$$p(d,g) = p(d|g)p(g)$$

and $p(d|g)$ represents the decision given the gender, i.e.

$$p(d|g) = \begin{cases} \text{Bernoulli}(\beta)(d) & \text{if $g=M$} \\ \text{Bernoulli}(\gamma)(d) & \text{if $g=F$} \end{cases}$$

in other words

$$p(d|g) = \mathbf{1}_{g=M} (\beta^d \cdot (1-\beta)^{1-d}) + \mathbf{1}_{g=F}(\gamma^d \cdot (1-\gamma)^{1-d})$$

and

$$p(g) = \alpha^{\mathbf{1}_{g=F}}(1-\alpha)^{\mathbf{1}_{g=M}}$$

or rather

$$p(d,g) = p(d|g) p(g) = \left[ \mathbf{1}_{g=M} (\beta^d \cdot (1-\beta)^{1-d}) + \mathbf{1}_{g=F}(\gamma^d \cdot (1-\gamma)^{1-d}) \right] \left( \alpha^{\mathbf{1}_{g=F}}(1-\alpha)^{\mathbf{1}_{g=M}} \right)$$