Suppose population A has $N_1$ members, and population B has $N_2$ members. There are $K$ common members in the populations. We want to estimate $K$.
Draw a sample of size $n$ from each population. Through comparing them, we find that these two samples have $k$ common members. How to estimate $K$?
I suppose that $N_1$, $N_2$, $n$ and $k$ are known.
However, in the original problem, both A and B are actually samples from two larger unknown overlapped but distinct populations.
My two cents:
Use maximum likelihood estimation on K:
Likelihood $P(data|N1, N2, K)\propto$ ${K\choose k} {N1-K \choose n-k} {N2-k \choose n-k}$
where nCr is the N-choose-k combinations.
Then find:
K_optimal = argmax(P w.r.t K)
I couldn't find an analytical solution so I wrote a few lines of code to calculate it, with an example like this:
from math import factorial
from scipy.special import comb
import seaborn as sns
N1 = 100
N2 = 180
n = 50
k = 25
def llhood(K):
return comb(K, k)*comb(N1-K, n-k)*comb(N2-K, n-k)
def argmaxK():
p = 0
i = k
arr = []
while i <= min([N1-n+k, N2-n+k]):
ll = llhood(i)
arr.append([i, ll])
if ll < p:
return i-1, arr
p = ll
i += 1
return i-1, arr
k_opt, probs = argmaxK()
probs = np.array(probs)
sns.scatterplot(probs[:,0], probs[:,1])
for my case, K is best estimated to be 45.
In a 2019 paper titled Bayes-optimal estimation of overlap between populations of fixed size, Daniel Larremore presents a solution when $N_1$ and $N_2$ are fixed and known. I'm not gonna repeat the whole paper and just present the main result. Without loss of generality, assume that $N_1 \leq N_2$. Further, denote $n_1$ and $n_2$ the number of samples drawn from populations $N_1$ and $N_2$ and $n_{12}$ the number of shared members in the sample. We also assume a uniform prior over $K$ (the true number of shared members), which is $p(K) = N_{1 + 1}^{-1}$. The posterior distribution is given by:
$$ P(K\,|\,n_1, n_2, n_{12}, N_1, N_2)=\dfrac{\sum_{K_1 = 0}^{N_1}P(n_{12}\,|\,n_2, K_1, N_2)P(K_1\,|\,n_1, K, N_1)}{\sum_{K'=0}^{N_1}\sum_{K_1=0}^{N_1}P(n_{12}\,|\,n_2, K_1, N_2)P(K_1\,|\,n_1, K', N_1)} $$ The posterior mean $\hat{K}$ is then given by:
$$ \hat{K}=\sum_{K=0}^{N_1}K\cdot P(K\,|\,n_1, n_2, n_{12}, N_1, N_2) $$
Here, $P(x\,|\,t, u, v)$ denotes the hypergeometric probability of drawing exactly $x$ special objects out of $t$ draws, from a population of size $v$, in which there are $u$ special objects total.
These formulas look quite complicated but they only require calls to the hypergeometric distribution which are available in many programs (R, Stata, SAS, Excel, etc.). Larremore provides Python code for the calculations on his GitHub page. Conservative equal-tailed $(1-\alpha)$-credible intervals $[K_{\mathrm{min}}, K_{\mathrm{max}}]$ can be found by finding the smallest index $K_{\mathrm{min}}$ and the largest index $K_{\mathrm{max}}$ for which $$ \sum_{K = K_{\mathrm{max}}}^{N_1}P(K\,|\,n_1, n_2, n_{12})\geq \alpha/2\\ \sum_{K = 0}^{K_{\mathrm{min}}}P(K\,|\,n_1, n_2, n_{12})\geq \alpha/2 $$
Example
To illustrate the formulas, let's calculate a concrete example. Assume that $N_1 = 75, N_2 = 100$ and $K = 35$. I randomly drew a sample of size $n_1 = n_2 = 40$ and got $n_{12} = 7$. The posterior distribution together with the posterior mean (orange point) and the $90$% credible interval (shaded blue region) looks like this:
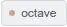
The true value of $K$ is indicated by a dashed vertical line. The posterior mean is $35.62$ and the $90$%-credible interval by $[20, 51]$.
To test the performance of the estimator, I repeated the above procedure $50$ times and recorded the posterior mean and $90$%-credible intervals. Here is the plot:
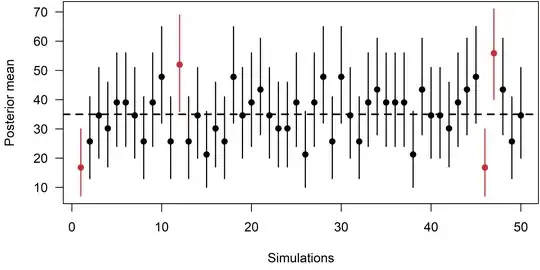
$4$ out of the $50$ credible intervals do not include the true $K$ of $35$ (they're plotted in red) and hence, $92$% do include it. Also, the mean of the $50$ posterior means is $35.19$.
