Determining standard deviations and standard errors for non-Gaussian distributions

Question

I have several questions about constructing error bars and using them as weights in the context of fitting, or indeed any kind of weighted statistic -- especially with regards to error and noise sources which are non-Gaussian.

Usually one might make a measurement, repeat it many times, and if the underlying source of error or noise on the measurement is Gaussian, then defining error bars and weights is relatively simple -- either some multiple of the standard deviation e.g. $\delta x = \pm \sigma$ encompasses $68\%$ of the data, OR a standard error like $\sigma/ \sqrt{n}$.

For example, I have constructed an arbitrary function and generated some random data with a Gaussian distribution: 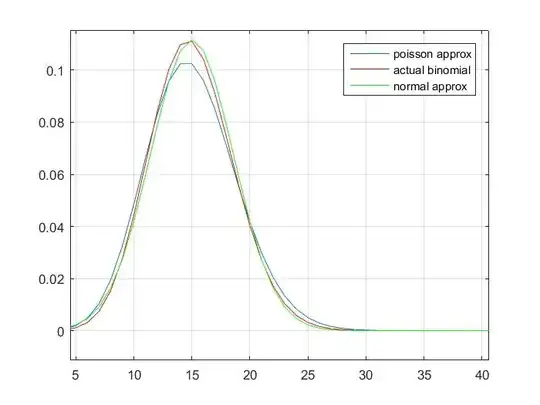The red plot markers indicate the mean, and the error bar is simply one standard deviation. I have plotted the corresponding PDF for each set of data and mapped these distributions to the plot. This is how I visualise the error and distribution of data, and what the mean data points (red markers) "really look like".

In the case of the Gaussian distribution the mode and the mean (expected value) are the same, but what about for other distributions, especially those that are asymmetrical. For example the Rayleigh distribution $$R(x) = \frac{x}{\sigma_{R}^{2}} e^{-x^{2}/(2 \sigma_{R}^{2})}$$ which has the shape parameter $\sigma_{R}$ which also defines its mode. Its mean is easily calculated via $$E(x) = \int_{0}^{+\infty} x R(x) \ \ dx$$ which gives the mean $$E(x) = \mu = \sigma_{R}\sqrt{\pi/2}$$ for the Rayleigh distribution. I show a plot of the Rayleigh distributions anatomy below where $\sigma_{R} = 1$:

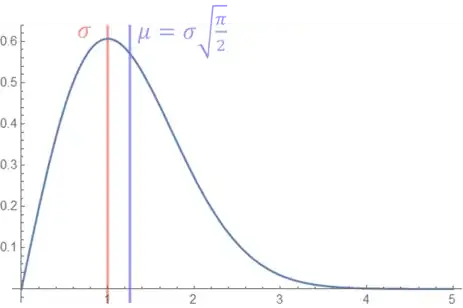
First question: As I understand it the variance, $\sigma^{2}$, may be calculated by $$V(x) = \sigma^{2} = \int_{-\infty}^{+\infty} (x - \mu)^{2} f(x)\ \ dx$$ where $\mu = E(x)$ as defined above. Does this mean the standard deviation for any distribution, $f(x)$, is simply $\sqrt{V(x)}$?

This to me is somewhat counter intuitive as for an asymmetric distribution I would expect an asymmetric standard deviation or error bar. If I repeat my example as above but this time using a Rayleigh distribution instead of a Gaussian: 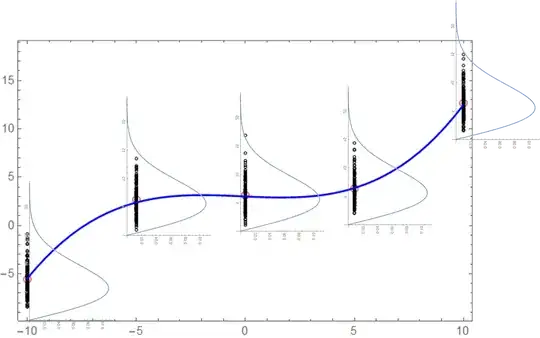I should stress this is a cartoon for how I am visualising the data

Second question: Should the standard deviation or error bars not reflect the shape of the distribution from which they are calculated? If one calculates the standard deviation using $$V(x) = \sigma^{2} = \int_{-\infty}^{+\infty} (x - \mu)^{2} f(x)\ \ dx$$ , it is clear that any error bar would be symmetric.

Third Question: Regardless of the answers to my first two questions, I would be curious to know how one would go about constructing a weight from an asymmetric error bar i.e. normally a weight is defined as $$W = 1/\sigma^{2}$$ where $\sigma$ can be the error or standard deviation in some quantity $x\pm \sigma$ where $\sigma$ could also be $\sigma = \delta x$ the error in some quantity. But what about if one has something like $$x^{+\delta x_{+}}_ {-\delta x_{-}}$$ where $\delta x_{-} < \delta x_{+}$. How would one construct a weight from this?

Answer 1

First question:

The "standard deviation" is defined mathematically, there is no other way to calculate it. It isn't meant to capture all the information about the shape of the distribution; no one numeric value could hope to do so except in the case of one-parameter distributions. Note that your expression for the variance:

$$V(x) = \sigma^{2} = \int_{-\infty}^{+\infty} (x - \mu)^{2} f(x)\ \ dx$$

does not specify the functional form of $f$; this means that the variance, and the standard deviation $\sigma$ (which is nothing more than $\sqrt{\sigma^2}$), are defined the same way regardless of $f$.

Second question:

The standard deviation does reflect one aspect of the shape of the distribution, namely, how spread out it is, writing loosely. Even then, it doesn't capture all aspects of what might be referred to as "spread out", e.g., those captured by kurtosis. It does not reflect skewness - the standard deviation of a random variable $x$ is the same as that of $-x$, although the skewness has switched signs, for example. If you want asymmetric error bars, which is in many cases a good thing to want, you'll have to construct them using either your knowledge of the distribution's functional form or other techniques such as bootstrapping; as you have realized, you can't get there from the standard deviation alone.

However, in many cases the Central Limit Theorem plus enough data and some assumptions means that even with non-normal errors, confidence intervals for individual parameters, e.g., regression coefficients, are well-approximated by a Normal distribution, for which symmetric confidence intervals are appropriate (unless you have an unusual criterion for your interval.)

Your Rayleigh distribution example above can be used to illustrate this; if I have a fair amount of data, my estimate of the Rayleigh parameter $\sigma_R$ will be approximately Normal (or $t$, with less data.) The random variate I'm observing will have a Rayleigh distribution, but the parameter estimate will not:

sr_hat <- rep(0,10000)

for (i in 1:10000) {
   x <- sqrt(-2*log(runif(100)))  # Rayleigh with parameter = 1
   sr_hat[i] <- mean(x*x)/2       # MLE of Rayleigh parameter
}

hist(sr_hat, xlab="MLE of Rayleigh(1) parameter", main="Histogram of ML Estimates")

which generates the following plot:

Not far from a Gaussian distribution, and further analysis (done at your leisure) will confirm this.

On the other hand, if you are trying to construct a predictive confidence interval, then you'd want to take the asymmetry of the Rayleigh distribution into account. There are lots of ways to do that; Bootstrap prediction interval, How to: Prediction intervals for linear regression via bootstrapping, and other questions may get you started on bootstrap methods. You can also generate pointwise confidence intervals for a curve, or for observations centered around a curve, as in your third plot above, through bootstrapping.

Here's a simple bootstrap for a predictive interval given a parameter estimate from 100 observations from a Rayleigh(1) distribution:

z <- rep(0,100000)

# Generate initial parameter estimate
x <- sqrt(-2*log(runif(100)))  # Rayleigh with parameter = 1
sr_est <- mean(x*x)/2          # MLE of Rayleigh parameter

# Bootstrap
for (i in 1:100000) {
   x <- sr_est * sqrt(-2*log(runif(100)))  # Rayleigh with parameter = sr_est
   sr_hat <- mean(x*x)/2                   # MLE of Rayleigh parameter
   z[i] <- sr_hat*sqrt(-2*log(runif(1)))
}

plot(density(z, bw="SJ", adjust=2), 
     xlab="Predictive distribution of Rayleigh(1) observations", 
     main = "Smoothed predictive density distribution", lwd=2)

which generates:

Third question:

If you are using squared-error loss, then generating weights using the variance is appropriate regardless of considerations of skew. To see this intuitively, consider the fact that squared error itself doesn't take skew into account, so one might suspect that optimal weighting of observations from a squared error perspective wouldn't either. How to estimate those weights when you don't know them a priori is a bigger issue; see the second answer to How do you find weights for weighted least squares regression? for an example of a situation where an optimal weighting scheme isn't dependent upon a variance estimate at all!

If, on the other hand, you aren't using squared-error loss, then $w_i = 1/\sigma^2_i$ may not be the appropriate weighting scheme, as you suspect. What would be an appropriate weighting scheme is going to be problem-specific, and, without further information, far beyond the scope of this answer.