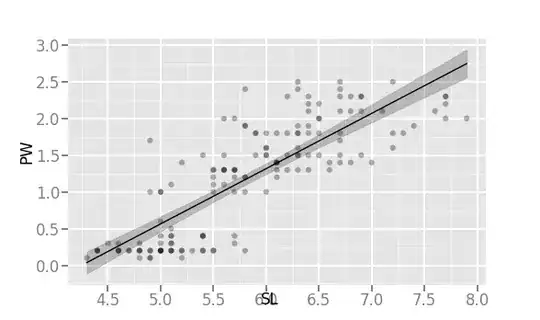
I am using ggplot with Python for showing regression/correlation. With method='lm' (means "linear model"), I get following graph:
And with method='loess', I get following:
The width of SE area is much wider with loess method than with lm method. Is this expected or is there an error somewhere?
Following is Python code to get above figures:
from ggplot import *
print (ggplot(aes(x='SL', y='PW'), data=irisdf) + \
geom_point(alpha=0.3) + \
stat_smooth(colour="black", se=True, method='lm'))
# or method='loess' in above line
plt.show()