I have the following problem:
Y = X + e
with
Y = Total reaction time (noisy signal)
X = selection time (signal)
e = discrimination time (noise)
I am interestend in the distribution for X and have only samples for Y and e. The experiment had unpaired samples for Y and e, thus I cannot use X=Y-e. Therefore I have to use deconvolution.
I have samples of reaction times (Y and e) for 16 participants (more than 1000 samples per participant). For deconvolution I have to assume that X and e are independend.
Intuitively I think that people with slower selection time X could also have a slower discrimination time. So I assume that there could be some kind of dependency between X and e (which would be a problem for the deconvolution).
My idea is to deconvolve the signal X for each participant separately (because I think that X and e should be independend for each participant) which leads to 16 deconvolved densities and than average those densities. So I hope to getting rid of the possible dependency between X and e.
The overall variance of the discrimination time (noise) is bigger than the variance of the noise for each single participant. Therefore applying deconvolution for all participants simultaneously may gives me a vague estimation for the signal X. Here I am not sure if a smaller variance for the noise e yields to a better deconvolved signal X? Applying deconvolution for each participant separately and than average them may yield to a more accurate estimate of the density X (because the variance of the noise for each participant is smaller).
Do you think that applying deconvolution separately will help me to get better results? Because I want to argue that deconvolving each density separately and than average them is better, I would like to know which argument 1. or 2. sounds better?
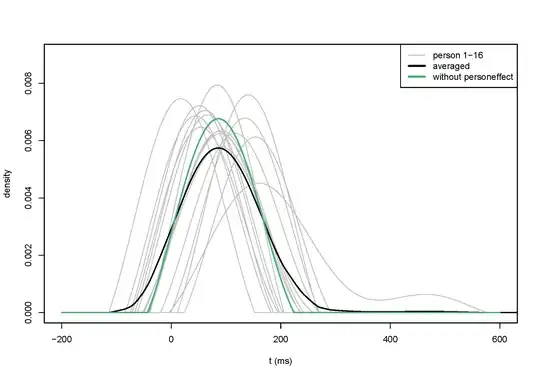
The following plot gives an example of the deconvolved densities. The gray ones are the 16 deconvolved densities for each participant, the black one is the averaged density over all 16 participants and the green one is the deconvolved density for all participants simultaneously.