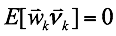I am reading 'Applied multivariate statistical analysis' by Richard Johnson and I do not understand that first to explain this test, talks about the t-student distribution.
And then out of nowhere he plugs the f-distribution:
I even read this post: Relationship between F and Student's t distributions
But, i am not able to follow the explanation. Why has he plugging the f-distribution out of nowhere? and if the result is a mix of t and f distributions, why isn't this a complete new distribution with a different name? (I would like to be able to understand this graphically)