There are three rooms with 40 identical boxes in each room. Each box contains some number of cards inside. The number of cards in each box is different. It may be as many as 60 cards in one box and as few as one card in one box.
Although the amounts of cards in each box of the same room are different, the sets of boxes in rooms are identical. That means that if in the room A there is a box containing, say, 39 cards, then there should also be a similar box with 39 cards in the room B, and another such one in the room C.
The set of boxes in each room is compiled as follows: the first box has only one card, the second one has two, the third one has three and so on until the 40th box (inclusive). The 40th box, thus, has 40 cards in it. So, the total number of cards in each room is 820 (1+2+3+4+5+6+7+…+37+38+39+40 = 820). However, the contestants don’t know the total number of cards in each room.
The boxes are placed on the floor in each room in a random order.
Now, three contestants are given the task – each one of them is asked to enter into his room and, using his intuition, within one minute to try to get a bigger number of cards than his contenders while opening the smaller number of boxes than his contenders.
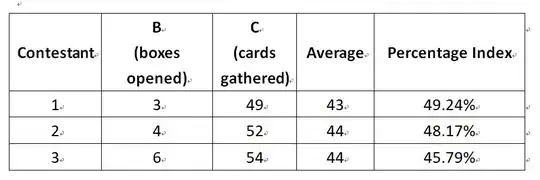
So, let's say they have done their jobs and their results are as follows:
Contestant 1 opened 3 boxes and gathered 49 cards from them;
Contestant 2 opened 4 boxes and gathered 52 cards from them;
Contestant 3 opened 6 boxes and gathered 54 cards from them;
Here each contestant comes up with at least two different results: the number of boxes he has opened – let’s denote it by “B”, and the number of cards he has gathered – let’s denote it by “C”.
Because each contestant has two numbers as a result (instead of just one number like in racing), I am a bit puzzled here as to how to decide the winner. I have thought of a number of ways:
1) Dividing the offset of B (which is 40-B) by C in each case and then comparing the resultant quotients:
(40-B1)/C1 ~ (40-B2)/C2 ~ (40-B3)/C3.
2) Dividing C by the offset of B in each case and then comparing the quotients:
C1/(40-B1) ~ C2/(40-B2) ~ C3/(40-B3).
3) Comparing the averages of C and the offset of B:
(C1+40-B1)/2 ~ (C2+40-B2)/2 ~ (C3+40-B3)/2.
4) Calculating the “percentage indices” (I don't know how to name them in English properly) and then comparing them. Here is how I calculate them:
Since we know the minimum and the maximum possible numbers of boxes that can be opened by one contestant, which are 1 and 40 respectively, and since we know the minimum and the maximum possible numbers of cards that one contestant can gather, which are 1 and 820 respectively, we can try calculating the percentage:
820/100 = 1%, which is 1% of the quality of the contestant “card performance” (the more cards are gathered, the better)
40/100 = 1%, which is 1% of the “anti-quality” of the contestant “box performance” (the more boxes are opened, the worse; “anti-quality” is the offset of quality: the anti-quality result “7 opened boxes” corresponds to the quality result “33 unopened boxes”, “8 opened boxes” corresponds to “32 unopened boxes”, and so on)
Thus, in case with contestant 1, whose B value equals to 3 (3 boxes opened) and whose C value equals to 49 (49 cards gathered), his percentage indices will look as follows:
%C1 = C1/(820/100) = 49/8.2 = 5.98%
%B1 = (40-B1)/(40/100) = (40-3)/0.4 = 92.5%
Now we can calculate the average of these two indices:
(%C1 + %B1)/2 = (5.98%/92.5%)/2 = 49.24%
The first two ways didn’t strike me as correct ones, but the last two seemed fine.
However, when I calculated the averages and the percentage indices for the three contestants, I got the following results:
As it can be seen from this table, if I take the “Average” way, then the second and third contestants will share the first place, while the first one will win silver. But if I take the “Percentage Index” way, then the first contestant will get gold, the second one silver, and the third one bronze!
So, the final results of the “Average” way are quite different from the “Percentage Index”. Why is this so?
Which way here is more correct, the “Average” or the “Percentage Index”?