How to test for main effects in 2x2 factorial design with categorical outcome

Question

The problem I have is as follows: I have a clinical trial based on 2x2 factorial design (four treatment combinations, balanced design)comparing treatment A with treatment B, where the primary outcome is dichotomous response variable, denoting patients' response to treatment (yes/no). A total of 100 patients were enrolled in the trial and the estimated response rates are below:

My question is, how do I perfom a test of the main effect of treatment A, for example and then test for interaction effect? I know that F or t-test is not appropriate, since my dependent variable is not continuous. My thoughts for how to do this are the following:

Since outcome is dichotomous, we have the logistic regression model:

$$logit(P) = α + \beta_Ax_1 + \beta_Bx_2 + \beta_{AB}x_1x_2$$

For main effect of A, null hypothesis: $\beta_A = 0$ vs alternative: $\beta_A ≠ 0$ and use chi-square test. Would that be appropriate given my relative small cell counts or would Fisher's Exact test be better? And if chi-square is ok, then would this be the correct formula to use to test for main effect of A or how should I do it?

$\chi^2 = [10 - (18*23/36)^2]/(18*23/36) + [8-(18*13/36)^2]/(13*18/36) + [13-(18*23/36)^2]/(18*23/36) + [5-(13*18/36)^2]/(13*18/36)$

Similarly, for interaction effect, null hypothesis: $\beta_{AB} = 0$ vs. alternative: $\beta_{AB} ≠ 0$ and again use chi-square/Fisher's test?

Any suggestions/help would be appreciated, thank you!

================================================================================ UPDATE: Ok, so I fitted a logistic model in R with glm and this was what I got:

It appears that the AB interaction effect is not significant according to p-value=0.2.

Question: Now in order to test for the main effect of treatment A and main effect of treatment B, do I have to fit two separate models, one just with treatment A (for main effect of A) like so: glm(cbind(no, yes)~treatmentA and then one just with B for the main effect of B or can I just take the p-values from the original model with the interaction term (p for A is 0.396; p for B is 0.556)? What would be the statistically valid way to do this?

Answer 1

If you are interested in the possibility of interaction between treatments A and B, you should be examining the interaction first, and what you call "main effects" later. If there is a significant interaction then there is no single effect of either A or B: there is an effect of each absent the other, and an effect of their combination. If there is no significant interaction then you might be justified in removing the interaction term from the analysis.

Logistic regression, including an interaction term, would be an obvious way to model this. (Fisher's exact test or the chi-square test for contingency tables are more like tests for interactions.) Instead of re-inventing the code, take advantage of standard, vetted, software packages to do the calculations. Such software will provide z-tests of the hypotheses that each of the regression coefficients (including for the interaction term) equals zero.

It's not clear that your study is sufficiently powered to answer your question cleanly, however. For logistic regression one usually wants to restrict analysis to 1 predictor (including interactions) per 15 or so cases in the smaller outcome category; looks like you only have about 30 responses to treatment in total (many of which seem to be in the no-treatment group) for 3 predictors (A, B, and A+B combination).

Added after seeing logistic regression results

As noted in a comment on your question there is still an issue about whether the outcomes have been coded correctly. It certainly seems surprising that the combination of treatments A and B would lead to a lower probability of "yes" outcomes than would the absence of treatment. That doesn't affect what follows, however, except for a reversal of signs of the coefficients.

First, if you had reason to suspect that the combination of A+B would affect the log-odds of outcome differently than the sum of their individual effects, then you were correct to include the interaction term in your model. In your model including the interaction, however, none of the estimated regression coefficient values is significantly different from 0. The magnitude of the interaction term nevertheless is greater than the magnitudes of the individual effects of A or B, consistent with it's having been wise to include the interaction. The interaction term is nominally the closest to "significant" of any. In this case some would argue that it is better to stay with the pre-specified model rather than remove the interaction term. Additional thoughts are on this page, this page, and many other pages on this site found via a search for "drop interaction term".

Second, even if it could be argued to proceed without the interaction term, in logistic regression it is dangerous to omit predictors that might be related for outcome, due to inherent omitted-variable bias. So the best analysis in that case would be a model combining treatments A and B but without the interaction term.* In that case the coefficient for B does come out nominally significant (p = 0.039), while the coefficient value for A is 0 (p = 1). The Wald test provided by the rms package in R (via anova(lrm())) for overall model significance is not, however, significant (p = 0.12). As these nominal p-values are based on the assumption that you did not look at the data to design the tests, you should be very cautious in attributing significance to the results. One benefit of statistical analysis is that it minimizes the chance that you will fool yourself into believing a false-positive finding, and in that way can prevent you from wasting further resources.

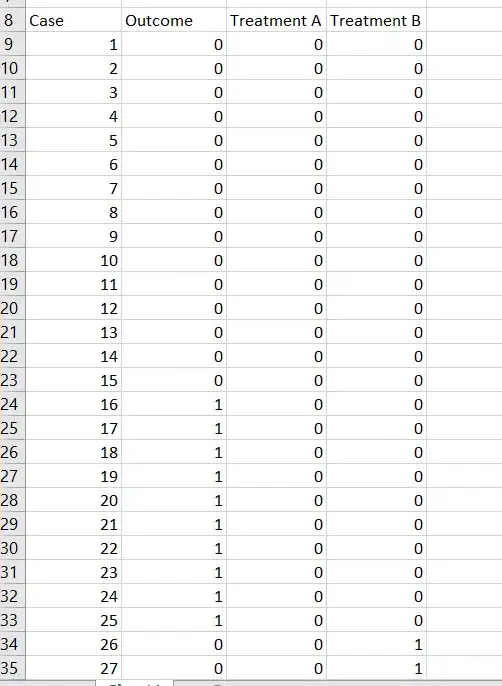
In terms of how to proceed, make sure that you have the outcomes coded correctly. You certainly don't want to be wasting time on treatment B if by itself it is worse than no treatment at all and if it's even less beneficial when combined with A. Yet that is what your initial table of probabilities and your frequency table suggest.

If your outcomes are coded/analyzed incorrectly (as I suspect), then your results at least aren't inconsistent with some effect of treatment B, an effect that might be enhanced by co-treatment with A. But you don't have enough data to make that claim reliably. If you need to write up your results to date, it might be best to show results both with and without the interaction term, while including some discussion of the pros and cons. For designing future work, you might want to explore in more detail both treatment B and its potential interaction with treatment A, informed both by these preliminary results and your knowledge of the subject matter.

---

*In your particular case the coefficients for the treatments and their individual p-values come out the same whether you do this as a combined 2-predictor analysis or as 2 separate single-predictor analyses. I think that's because the coefficient for A comes out to be 0 and you have a balance design. But in more general cases that won't be the case, hence the recommendation for a combined analysis as the default.

Answer 2

Rather than expressing this in terms of the proportions, it is better to deal directly with the underlying count data. You essentially have a $2 \times 2 \times 2$ contingency table of count values, so you should be looking at tests of partial independence for that kind of data. Since you have small count values, it is probably feasible to use a Fisher exact test on this data, so long as you can find an appropriate facility for a three-dimensional table. I would suggest you look up some resources on partial independence tests for a $2 \times 2 \times 2$ contingency table, and decide which test you would like to implement.

Answer 3

@EdM. So, you're basically saying I should create a table with 100 rows and 3 columns corresponding to outcome, treatment A and treatment B and then do the logistic regression on that? Something like this?