Recently, I read papers that perform power-law fitting on their empirical data (estimate the alpha), some of them report corresponding p-value for the Kolmogorov-Smirnov test, but many of them do not.
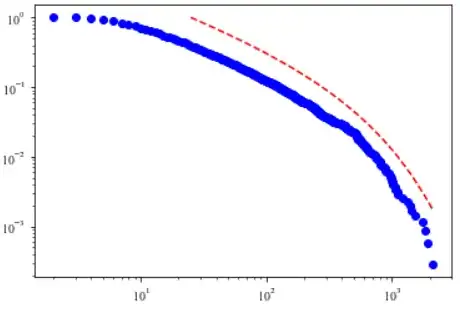
I am completely new to this kind of work and I am able to perform power-law fitting thanks to the program from Clauset et al. However, according to the K-S test and its corresponding p-value, my data seems doesn't follow a pure power-law distribution.
Then I use the python program powerlaw to do a truncated power-law fit, which seems a better fit visually, but this package doesn't provide a K-S test function.
And my question is:
- How to perform a Kolmogorov-Smirnov test on the truncated power-law distributed data? or maybe other tests?
- How to estimate the xmax of a truncated power-law?
- Is it normal that a power-law fitted line does not go through the data points, but lies above them?
I think this is a very hard problem for me, is there some concrete tutorial on data fitting and testing?
Here is my data and the power-law fitted line (alpha=1.92)
⬇ My data and the truncated power-law fitted line (alpha=1.66, beta=0.0009)
⬇ The truncated power-law fit of the data from a paper
