3

Say I have two models (classifiers), $M_1$ and $M_2$, each with their own accuracy w.r.t. the ground truth, and I calculate also Cohen's Kappa between each model and the ground truth (as a measure of agreement between model predictions and ground truth).

Can I expect that the model with higher accuracy will also have a higher Cohen's Kappa, i.e. better agreement with ground truth? How can I prove (or refute) this?

ttnphns
  • 51,648
  • 40
  • 253
  • 462
vbn
  • 33
  • 5
  • Kappa is a measure of interrater reliability. Accuracy (at least for classifiers) is a measure of how well a model classifies observations. They aren't comparable quantities. – Peter Flom Dec 15 '19 at 17:22
  • @PeterFlom-ReinstateMonica Could you at least give me an example (for the same case) where increasing accuracy provokes a decrease in kappa? For me that's enough, I have been unable to find one. – vbn Dec 16 '19 at 07:20
  • The term "the kappa of M1" is meaningless. Cohen's Kappa is a relation between two models. You can ask about the Kappa of M1 and M2, for example. – Itamar Mushkin Dec 16 '19 at 07:28
  • Theoretically, you can ask about the "Kappa of M1 and the ground truth". In this case, You see from the link you've shared about Cohen's Kappa that it is just a modified accuracy - it is equal to (p_0 -p_e)/(1-p_e), where p_0 is just the accuracy. So, no, if you ask about "the Kappa of M1 and the ground truth", then there is no situation in which an increase in accuracy provokes a decrease in this (probably ill-named) Kappa. – Itamar Mushkin Dec 16 '19 at 07:30
  • @ItamarMushkin Could you please make a more formal demonstration? I have been unable to make one. – vbn Dec 16 '19 at 08:25
  • @ItamarMushkin Yeah, the comparison it's between the model and the ground truth. It's how it's used normally in machine learning so it was obvious to me. – vbn Dec 16 '19 at 08:27
  • 1. If this is the usage you meant, please edit your question accordingly. I did not get that use, and it took me a while to find something similar online (here: https://thedatascientist.com/performance-measures-cohens-kappa-statistic/ - one rater is just guessing according to class frequency). – Itamar Mushkin Dec 16 '19 at 10:16
  • 2. After you edit your question and it's clear enough to be reopened, I'll try elaborating a bit more, bur really there's nothing more to it than what I've said in my comment. – Itamar Mushkin Dec 16 '19 at 10:17
  • I've suggested an edit in agreement with what you've asked in comments. Feel free to elaborate or correct it. – Itamar Mushkin Dec 16 '19 at 10:22
  • No, I can't, because they measure different things. It's like saying "Can you give me an example where raising the temperature increases length?" – Peter Flom Dec 16 '19 at 10:51
  • @ItamarMushkin I have accepted your edit, it was exactly what I meant. The demonstration is not necessary to be too complex or too formal, a small explanation it's enough. – vbn Dec 16 '19 at 13:03
  • In that case, I gave the explanation in a previous comment: in that case, Cohen's Kappa is just equal to (p_0 -p_e)/(1-p_e), where p_0 is just the accuracy. So, it increases monotonically with accuracy. That's it. – Itamar Mushkin Dec 16 '19 at 13:42
  • I hope that the question (after my edit) will be re-opened, so I can move the answer from comments to answer (and delete most of the comments, or at least mine). – Itamar Mushkin Dec 16 '19 at 13:43
  • @PeterFlom-ReinstateMonica Please re-open the question now it's clear what I want. – vbn Dec 16 '19 at 16:57
  • @ItamarMushkin But p_e also changes when accuracy changes. – vbn Dec 16 '19 at 17:00
  • @ItamarMushkin Any ideas? – vbn Dec 18 '19 at 09:13
  • The more I search, the less I understand how to use Cohen's Kappa to compare an estimator to the ground truth. The SKLearn page warns explicitly against this: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.cohen_kappa_score.html – Itamar Mushkin Dec 23 '19 at 12:36
  • The accepted answer here touches on your question: https://stats.stackexchange.com/questions/303149/cohens-kappa-as-a-classifier-strength-estimator?rq=1, specifically look at the part about how to compute p_e – Itamar Mushkin Dec 23 '19 at 14:26

2 Answers2

5

Preliminary comments

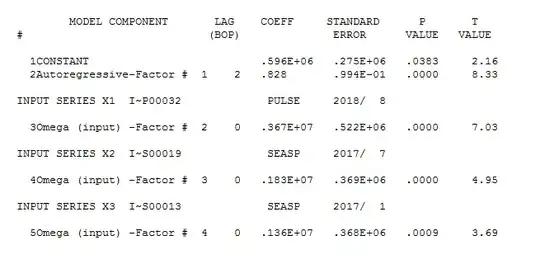
Cohen's Kappa is a multiclass classification agreement measure. It is Multiclass Accuracy measure (aka OSR) "normalized" or "corrected" for the chance agreement baseline. There exist other alternatives how to do such "correction" - for example, Scott's Pi measure. Below is an excerpt from my document describing my !clasagree SPSS macro, a function calculating many different measures to assess/compare classifications (the complete Word document is found in "Compare partitions" collection on my web-page). The excerpt below displays formulae for the currently available multiclass classification measures:

enter image description here

Accuracy as it is is a Binary or Class-specific classification agreement measure. It is computed not for all classes at once but for each class-of-interest. Having been computed for each class k of the K-class classification, it then can - if you wish - be averaged over the K classes to yield a single value. Below is again a portion of my aforementioned document now introducing some of a lot of binary classification measures:

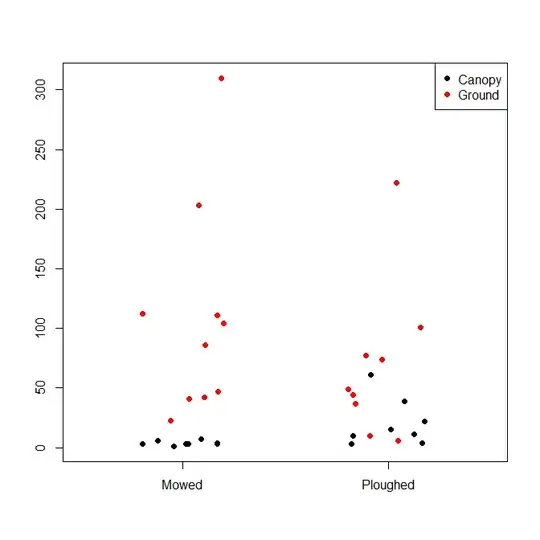
enter image description here

Now to note: When K=2, that is, there are only two classes, then the average binary Accuracy is the same as the Multiclass Accuracy (aka OSR). In general, when K, the number of existing classes, is the same in both classifications being compared, mean binary Accuracy and Multiclass Accuracy (OSR) are linearly equivalent (correlate with r=1).

Answer to the question

The following simulation experiment refutes the notion that Accuracy and Cohen's Kappa are monotonically related. Because your question is narrowed to K=2 class classification, the simulation creates random classifications with only two classes each. I thus simply generated independently 101 2-value variables. One of the variables I arbitrarily appointed to represent "True" classification and the other 100 to be alternative "Predicted" classifications. Because I did not generate the variables as correlated, the 100 classifications can be seen just random, blind "classifiers". I could have made them better than random by generating positively correlated variables - but that wouldn't drastically change the conclusion. I did not fix marginal counts, so classes were let to be moderately unbalanced.

The results of the comparisons of every of the 100 randomly built classifications (clas1 - clas100) with the "True" classification are below:

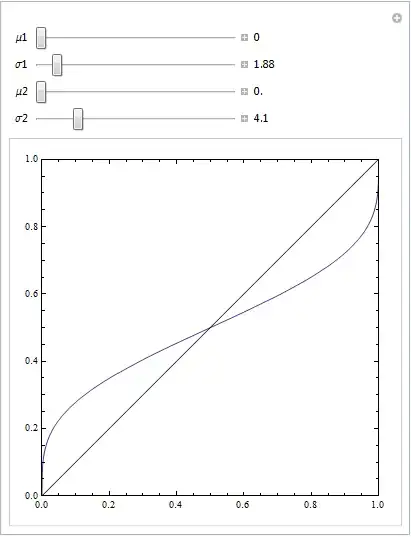
enter image description here

Binary Accuracy measure, after averaging its two values, is equal to Multiclass Accuracy (OSR), as was remarked earlier. Values of Kappa are generally low - but that is because our "classifiers" were on the average not better than random classifiers. The scatterplot of Kappa vs Accuracy:

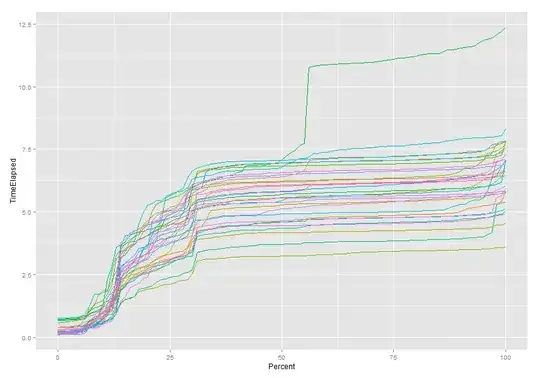
enter image description here

As you see, there is no any monotonic functional relation; hardly even any correlation at all. Conclusion: One should, generally, not expect that "the model with higher accuracy will also have a higher Cohen's Kappa, i.e. better agreement with ground truth".

Addition. I also generated 100 classifications that are better than random classifiers w.r.t. the "True" classification. That is, I generated 2-value variables, as before, now positively correlated (with some random $r$ ranging within 0.25-1.00) with the "True" classification variable. The scatterplot of Kappa vs Accuracy from this simulation:

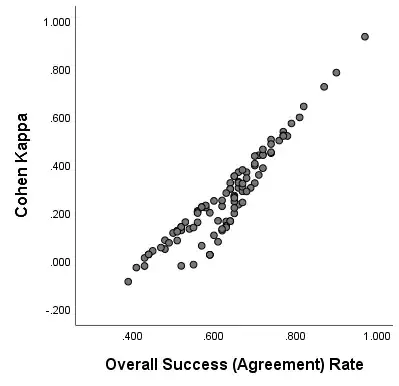
enter image description here

As seen, only at very high levels of agreement between a Predicted and the True classification the relation between Kappa and Agreement approaches monotonicity.

Community
  • 1
ttnphns
  • 51,648
  • 40
  • 253
  • 462
4

Kappa is a chance-adjusted index of agreement. Chance-adjusted indexes will always be equal to or lower than accuracy for the same data. You can prove this by looking at the formula for kappa.

$\kappa=\frac{p_o-p_c}{1-p_c}$

Where $p_o$ is percent observed agreement (i.e., accuracy) and $p_c$ is the estimated percent chance agreement. Given that percentages range from 0 to 1, $\kappa$ can achieve its highest value and be equal to $p_o$ when $p_c$ is 0. To the extent that $p_c$ is larger than 0, $\kappa$ will be smaller than $p_o$ or accuracy.

enter image description here

In the chart above, you can see that $\kappa=p_o$ when $p_c=0$ (the dark blue line along the diagonal) but as $p_c$ increases (the lighter blue lines) $\kappa<p_o$.

So, kappa will be lower than accuracy for the same data. But since you are comparing two different classifiers/coders, the data will change somewhat. The trusted labels should be the same for both, but the predictions will differ and therefore the chance agreement estimate may differ as well. This may lead to some strange behavior, especially if the class distributions (i.e., the percentage of objects assigned to each class) are very different between classifiers/coders. But in general kappa will be lower.

Jeffrey Girard
  • 3,922
  • 1
  • 13
  • 36