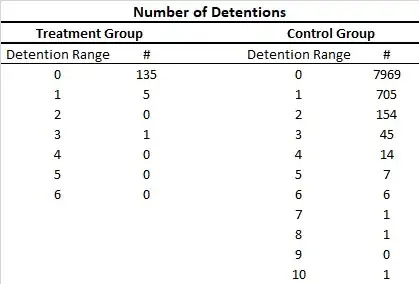
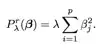2

I've conducted a study to see if an intervention has decreased the number of detentions a sample of students obtains. Out of roughly 9000 students at a very large middle school I randomly selected 141. Before school started they participated in an intervention. After the Fall semester I obtained the number of detentions each student obtained. Table Below.

enter image description here

I want to see if the treatment group had a significantly smaller number of detentions than the control group.

A statistics friend of mine recommended that my data comes from a Poisson distribution and I'm looking into it. But I'd like to find some advice from this forum as well.

Ryan Doherty
  • 81
  • 5
  • Why is the characterization of an underlying distribution relevant to your research objective? – whuber Dec 04 '19 at 17:34
  • @whuber, I think the person wants to figure out what test is appropriate for data not follows a normal distribution. Hope I am right. – Bill Chen Dec 04 '19 at 17:36
  • @Bill I need to reiterate my question, then: because it was obvious at the outset that these data wouldn't possibly follow a normal distribution, why could it be relevant to test whether they follow a Poisson distribution? – whuber Dec 04 '19 at 17:37
  • @whuber edited answer. – Bill Chen Dec 04 '19 at 17:45

2 Answers2

3

Sometimes a result is obvious. In this case, 10.5% of the people in the control group received detentions. In your sample of 141, only 6 received detentions. The chance of six or fewer detentions in any random sample of 141 from the control group is given by the Binomial distribution with parameters 141 and 0.105; a calculation gives it as 0.63%, which is low. However, the value of 10.5% is a little uncertain. The right way to make this comparison is with a one-sided test of proportions. It gives a p-value of 1.17%, low enough to provisionally conclude your treatment group is unlike the control: significantly fewer people got detentions.

However, your question actually is about the numbers of detentions rather than how many people received them. Although you could try to use a test that assumes the underlying distributions are Poisson, there is strong evidence they are not. The check is simple: the average number of detentions per student in both groups is $0.14463$ and the Poisson distribution with that average doesn't reproduce either set of data accurately. In particular, the Poisson distribution with this mean tells us to expect around 19 detentions in the study group (there were only 8) and to expect no people had more than four detentions in the control group (there 30 of them). You could apply a formal test, such as a chi-squared test, but the result is so obvious that there's no need: abandon the Poisson hypothesis.

That brings us to the ultimate question: are your data consistent with a hypothesis of no intervention effect? A simple way to assess that is to draw many samples of size 141 from the control group and compare their detention counts to the eight in the study group. Here are the results of a million such samples:

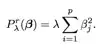
Figure

Almost all of these million random samples had more than eight detentions (as marked by the vertical red bar). Only 0.97% of them had eight or fewer. This is moderately good evidence that the intervention lowered the number of detentions.

whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • Why is the value of 10.5% a little uncertain? Isn't the total student body of around 9K people a population? And if so isn't that a correct expected value? – Ryan Doherty Dec 04 '19 at 20:22
  • 1
    The 9K people ought to be viewed as sample of a process, not a population. To see why, suppose your intervention group contained 9K people and the control group was left with only 100 people: would you still view its data as a population and its results as being absolutely certain? Presumably not--but the size of a dataset does not determine whether it's a sample or a population. – whuber Dec 04 '19 at 21:05
  • to find the p-value would I essentially do in R: binom.test(6,141,p=.105) – Ryan Doherty Dec 05 '19 at 15:15
  • 1
    That will give you twice the value of 0.63% I quoted, because it's a two-sided test. It's a reasonably conservative answer. Remember, though, that it doesn't exactly answer the question you posed: it compares numbers of *students* rather than numbers of *detentions.* – whuber Dec 05 '19 at 15:50
0

The reason why your friend told you it's following a Poison distribution, is that hypothesis testings have assumptions. So to test the difference between two means if the data from two normal distribution, the t-test is the first choice.

Since the Poisson distribution is entirely determined by its parameter, so a hypothesis test would be a test of equality of their mean parameter, which will conclude whether the two data from the same distribution or not. If they are, then your treatment doesn't affect.

One possible test is poisson.test on two samples in R

Reference: What is a statistical significance test for two Poisson distributions?

Hope this helps.

Bill Chen
  • 250
  • 2
  • 8