Why does VGG16 use 13 hidden layers, rather 12 hidden layers, or maybe 10 hidden layers? What is the motivation of the architecture?
I think that maybe if we use only 12 hidden layers, similar performance could be achieved.
I want to know the motivation of the deep neural networks' architecture, but almost all the deep neural networks are too complex to understand the motivation behind them.
In the published article about VGG, the authors explain that:
Our main contribution is a thorough evaluation of networks of increasing depth using an architecture with very small ($3\times3$) convolution filters, which shows that a significant improvement on the prior-art configurations can be achieved by pushing the depth to $16$–$19$ weight layers.
(Emphasis mine)
They did so by fixing all the other parameters of the ConvNet architecture and gradually increasing the number of hidden layers.$^\dagger$ Of course, all other things constant, the deeper the network, the more memory it takes to store and the longer it takes to train. They used the minimal filter size that still preserves direction ($3\times3$) to counteract this.
The answer to your question therefore boils down to: Because the deeper configurations outperformed shallower ones in their comparison. This has likely to do with the ability of deeper networks to make increasingly complex abstractions of the original input (pixel intensities). Here is a great answer as to why deep networks generally outperform shallow ones.
Why theirs does specifically is also addressed in the paper: Up until then, the state-of-the-art architectures used relatively large convolutions. However, two consecutive $3\times3$ convolutional layers with stride $1$ have the same effective receptive field as one $5\times5$ convolutional layer, but with fewer parameters. Three consecutive layers have an effective receptive field of a $7\times7$. For $C$ channels, the number of parameters is almost halved:
$$\text{One } (7\times7) \text{ layer}: \,\qquad 7^2C^2 = 49C^2\\ \text{Three } (3\times3) \text{ layers}: \quad 3^3C^2 = 27C^2$$
In addition to having far fewer parameters, you now also benefit from three non-linear activations.
$\dagger$: In fact, the configurations they compare on the ImageNet challenge range all the way from $11$ to $19$ layers:
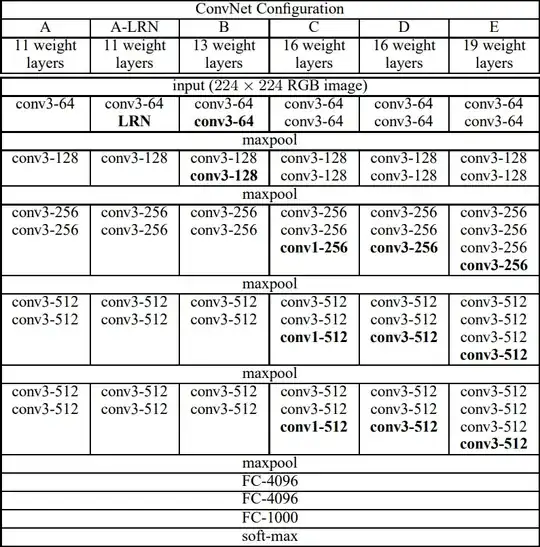
The configuration you are referring to is either C or D.
K. Simonyan, A. Zisserman (2015): Very Deep Convolutional Networks for Large-Scale Image Recognition International Conference on Learning Representations