Are random variables correlated if and only if their ranks are correlated?

Question

Assume $X,Y$ are continuous random variables with finite second moments. The population version of Spearman's rank correlation coefficient $ρ_s$ can be defined as the Pearson's product-moment coefficient ρ of the probability integrals transforms $F_X(X)$ and $F_Y(Y)$, where $F_X,F_Y$ are the cdf's of $X$ and $Y$, i.e.,

$ρ_s(X,Y)=ρ(F(X),F(Y))$.

I wonder whether one can generally conclude that

$ρ(X,Y)≠0↔ρ(F(X),F(Y))≠0$?

I.e., do we have linear correlation if and only if we have linear correlation between the ranks?

Update: In the comments two examples are given why

$\rho(F_X(X),F_Y(Y))=0\rightarrow \rho(X,Y) = 0$

is not true in general, even if $X$ and $Y$ have the same distribution. So the question should be reformulated as

$\rho(X,Y) = 0 \rightarrow \rho(F_X(X),F_Y(Y))$?

It is also of great interest to me whether this is true/false if $X$ and $Y$ have the same distribution.

(Note: If $X$ and $Y$ are positively quadrant dependent, i.e., $δ(x,y)=F_{X,Y}(x,y)−F_X(x)F_Y(y)>0$ then Hoeffding's covariance formula $Cov(X,Y)=∫∫δ(x,y)dxdy$ yields that $ρ(X,Y)>0$ and $ρ(F(X),F(Y))>0$.)

Answer 1

Neither correlation being zero necessarily tells you much about the other, since they 'weight' the data - especially extreme data - quite differently. I am just going to play with samples, but similar examples could be constructed with bivariate distributions / copulas.

1. Spearman correlation 0 doesn't imply Pearson correlation 0:

As mentioned in the question, there are examples in the comments, but the basic structure is "construct a case where Spearman correlation is 0, then take an extreme point and make it more extreme without changing the Spearman correlation"

The examples in comments cover that very well, but I am just going to play with a more 'random' example here. So consider this data (in R), which by construction has both Spearman and Pearson correlation 0:

x=c(0.660527211673069, 0.853446087136149, -0.00673848667511427, 
-0.730570343152498, 0.0519171047989013, 0.00190761493801791, 
-0.72628058443299, 2.4453231076856, -0.918072410495674, -0.364060229489348, 
-0.520696233492491, 0.659907250608776)
y=c(-0.0214697990371976, 0.255615059485107, 1.10561181413232, 0.572216886959267, 
-0.929089680725018, 0.530329993414123, -0.219422799586819, -0.425186120279194, 
-0.848952532832652, 0.859700836483046, -0.00836246690850083, 
1.43806947831794)

cor(x,y);cor(x,y,method="sp")
[1] 1.523681e-18
[1] 0

Now add 1000 to y[12] and subtract 0.6 from x[9]; the Spearman correlation is unchanged but the Pearson correlation is now 0.1841:

  ya=y
  ya[12]=ya[12]+1000
  xa=x
  xa[9]=xa[9]-.6
  cor(xa,ya);cor(xa,ya,method="sp")
[1] 0.1841168
[1] 0

(If you want strong significance on that Pearson correlation, just replicate the entire sample several times.)

2. Pearson correlation 0 doesn't imply Spearman correlation 0:

Here's two examples with zero Pearson correlation but nonzero Spearman correlation (and again, if you want strong significance on these Spearman correlations, just replicate the entire sample several times).

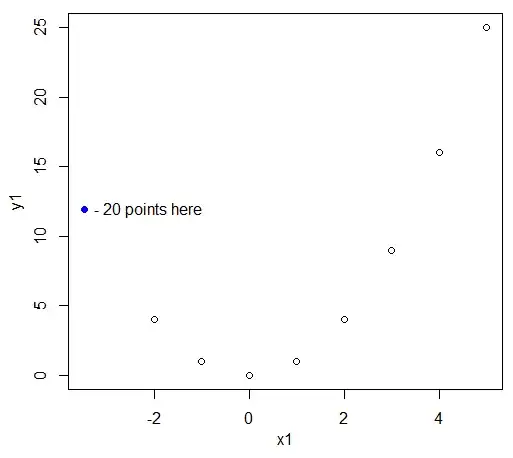
Example 1:

 x1=c(rep(-3.4566679074320789866,20),-2:5)
 y1=x1*x1
 cor(x1,y1);cor(x1,y1,method="spe")
[1] -8.007297e-17 
[1] -0.3512699   

Example 2:

 k=16.881943016134132 
 x2=c(-9:9,-k,k)
 y2=c(-9:9,k,-k)
 cor(x2,y2);cor(x2,y2,method="spe")
[1] -9.154471e-17
[1] 0.4805195

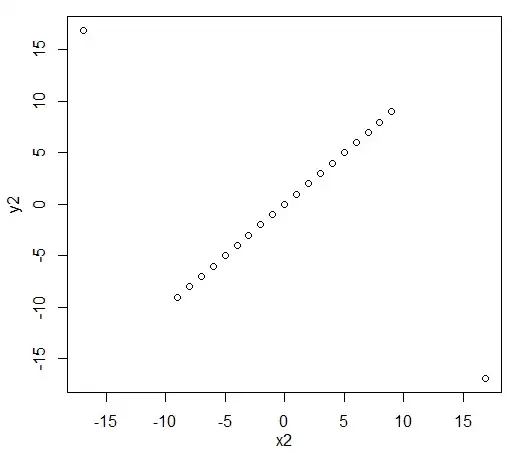
In this last example, the Spearman correlation can be made stronger by adding more points on y=x while making the two points at the top left and bottom right more extreme to maintain the Pearson correlation at 0.