Illustrations of previous comments.
Normal approximation to binomial.
A commonly used rule of thumb is that $np > K$ and $n(1-p) > K$ for some $K.$
In your question, $K = 10,$ but values $K = 5, 9, 20$ are also commonly quoted.
The purposes of this and other 'rules of thumb' are to use a normal
approximation only when the binomial distribution at hand has $n$ large
enough for the CLT to have some effect, for $p$ to be 'relatively' close
to $1/2$ so that the binomial is not too badly skewed, and to make sure
that the approximating normal distribution puts almost all of its
probability between $0$ and $n.$ The hope is to approximate probabilities
of events accurately to about two decimal places.
I will illustrate with $n = 60$ and $p = 0.1,$ a case that meets the rule
you mention for $K = 5$ but not for $K = 10.$
So for $X \sim \mathsf{Binom}(n = 60, p = .1),$ let's evaluate
$P(2 \le X \le 4) = P(1.5 < X < 4.5).$ The exact value $0.2571812$ is easily obtained
in R statistical software, using the binomial PDF dbinom or the binomial CDF pbinom.
sum(dbinom(2:4, 60, .1))
[1] 0.2571812
diff(pbinom(c(1,4), 60, .1))
[1] 0.2571812
The 'best-fitting' normal distribution has $\mu = np = 6$ and
$\sigma = \sqrt{np(1-p)} = 2.32379.$ Then the approximate value $0.2328988$ of the target probability, using the 'continuity correction' is obtained in R as follows:
mu = 6; sg = 2.32379
diff(pnorm(c(1.5,4.5), mu, sg))
[1] 0.2328988
So we do not quite get the desired 2-place accuracy. You could get almost the same normal approximation by standardizing and using
printed tables of the standard normal CDF, but that procedure often involves
some minor rounding errors. The following figure shows that the 'best fitting' normal distribution is not exactly a good fit.
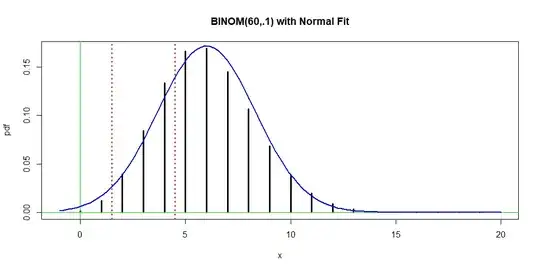
x = 0:20; pdf = dbinom(x, 60, .1)
plot(x, pdf, type="h", lwd = 3, xlim= c(-1,20),
main="BINOM(60,.1) with Normal Fit")
abline(h=0, col="green2"); abline(v=0, col="green2")
abline(v = c(1.5,4.5), col="red", lwd=2, lty="dotted")
curve(dnorm(x, mu, sg), add=T, lwd=2, col="blue")
For most practical purposes it is best to use software to compute an exact
binomial probability.
Note: A skew-normal approximation. Generally speaking, the goals of the usual rules of thumb for
successful use of the normal approximation to a binomial probability are based on avoiding cases where the relevant binomial distribution is too skewed for a good normal fit. By contrast, J. Pitman (1993): Probability, Springer, p106, seeks to accommodate to skewness in order to achieve a closer approximation, as follows. If $X \sim \mathsf{Binom}(n,p),$ with $\mu = np,$ and $\sigma = \sqrt{np(1-p)},$ then
$$P(X \le b) \approx \Phi(z) - \frac 16 \frac{1-2p}{\sigma}(z^2 -1)\phi(z),$$
where $z = (b + .5 -\mu)/\sigma$ and $\Phi(\cdot)$ and $\phi(\cdot)$ are, respectively, the standard normal CDF and PDF. (A rationale is provided.)
In his example on the next page with $X \sim \mathsf{Binom}(100, .1),$ the exact binomial probability is $P(X \le 4) = 0.024$ and the usual normal approximation is $0.033,$ whereas the bias-adjusted normal approximation is $0.026,$ which is closer to the exact value.
pbinom(4, 100, .1)
[1] 0.02371108
pnorm(4.5, 10, 3)
[1] 0.03337651
pnorm(4.5, 10, 3) - (1 - .2)/18 * (z^2 - 1)*dnorm(z)
[1] 0.02557842
Normal approximation to Student's t distribution.
The figure below shows that the distribution $\mathsf{T}(\nu = 30)$
[dotted red] is nearly $\mathsf{Norm}(0,1)$ [black]. At the resolution of this graph, it is difficult to distinguish between the two densities. Densities of t with degrees of freedom 5, 8, and 15 are also shown [blue, cyan, orange].
Tail probabilities are more difficult to discern on this graph.
Quantiles .975 of standard normal (1.96) and of $\mathsf{T}(30)$ are both near $2.0.$ Many two-sided tests are done at the 5% level and many two-sided confidence intervals are at the 95% confidence level. This has given rise to the 'rule of thumb' that standard normal and
$\mathsf{T}(30)$ are not essentially different for purposes of inference. However, for tests at the 1% level and CIs at the 99% level, the number of degrees of freedom for nearly matching .995 quantiles is much greater than 30.
qnorm(.975)
[1] 1.959964
qt(.975, 30)
[1] 2.042272
qnorm(.995)
[1] 2.575829 # rounds to 2.6
qt(.995, 70)
[1] 2.647905 # rounds to 2.6
The legendary robustness of the t test against non-normal data is
another issue. I know of no sense in which a 'rule of 30' provides
a useful general guide when to use t tests for non-normal data.
If we have two samples of size $n = 12$ from $\mathsf{Unif}(0,1)$ and
$\mathsf{Unif}(.5,1.5),$ respectively, a Welch t test easily distinguishes between them, with power above 98%. (There are better tests for this.)
pv = replicate(10^6, t.test(runif(12),runif(12,.5,1.5))$p.val)
mean(pv < .05)
[1] 0.987446
Moreover, if we have two samples of size $n = 12$ from the same uniform
distribution, then the rejection rate of a test at the nominal 5% level is truly about 5%. So for such uniform data it doesn't take sample sizes as large as 30 for
the t test to give useful results.
pv = replicate(10^6, t.test(runif(12),runif(12))$p.val)
mean(pv < .05)
[1] 0.05116
By contrast, t tests would not give satisfactory results for samples of size 30 from exponential populations.
Note: This Q&A has relevant simulations in R.

