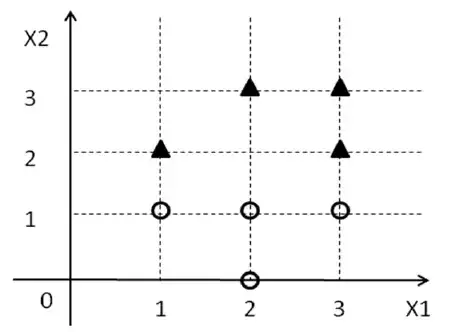
There are at least two ways to motivate SVMs, but I will take the simpler route here.
Now, forget everything you know about SVM for the moment and just focus on the problem at hand. You are given a set of points $\mathcal{D} = \{(x^i_1, x^i_2, y_i)\}$ along with some labels ($y_i$) which are from $\{1, -1\}$. Now, we are trying to find a line in 2D such that all points with label $1$ fall on one side of the line and all points with label $-1$ fall on the other side.
First of all, realize that $w_0 + w_1x_1 + w_2x_2 = 0$ is a line in 2D and $w_0 + w_1x_1 + w_2x_2 > 0$ represents "one side" of the line and $w_0 + w_1x_1 + w_2x_2 < 0$ represents the "other side" of the line.
From the above we can conclude that we want some vector $[w_0, w_1, w_2]$ such that,
$w_0 + w_1x^i_1 + w_2x^i_2 \geq 0$ for all points $x^i$ with $y_i = 1$ and $w_0 + w_1x^i_1 + w_2x^i_2 < 0$ for all points $x^i$ with $y_i = -1$ [1].
Let us assume that such a line actually exists then I can define a classifier in the following way,
$$
\min |w_0| + |w_1| + |w_2| \\
\text{subject to} : w_0 + w_1x^i_1 + w_2x^i_2 \geq 0, \forall x^i\text{ with }y_i = 1 \\
w_0 + w_1x^i_1 + w_2x^i_2 < 0, \forall x^i\text{ with }y_i = -1 \\
$$
I have used an arbitrary objective function above, we don't really care at the moment which objective function is used. We just want a $w$ that satisfies our constraints. Since we have assumed that a line exists such that we can separate the two classes with that line, we will find a solution to the above optimization problem.
The above is not SVM but it will give you a classifier :-). However this classifier may not be very good. But how do you define a good classifier? A good classifier is usually the one which does well on the test set. Ideally, you would go over all possible $w$'s that separate your training data and see which of them does well on the test data. However, there are infinite $w$'s, so this is quite hopeless. Instead, we will consider some heuristics to define a good classifier. One heuristic is that the line that separates the data will be sufficiently far away from all points (i.e there is always gap or margin between the points and the line). The best classifier amongst these is the one with the maximum margin. This is what gets used in SVMs.
Instead of insisting that $w_0 + w_1x^i_1 + w_2x^i_2 \geq 0$ for all points $x^i$ with $y_i = 1$ and $w_0 + w_1x^i_1 + w_2x^i_2 < 0$ for all points $x^i$ with $y_i = -1$, if we insist that $w_0 + w_1x^i_1 + w_2x^i_2 \geq 1$ for all points $x^i$ with $y_i = 1$ and $w_0 + w_1x^i_1 + w_2x^i_2 \leq -1$ for all points $x^i$ with $y_i = -1$, then we are actually insisting that points be far away from the line. The geometric margin corresponding to this requirement comes out to be $\frac{1}{\|w\|_2}$.
So, we get the following optimization problem,
$$
\max \frac{1}{\|w\|_2} \\
\text{subject to} : w_0 + w_1x^i_1 + w_2x^i_2 \geq 1, \forall x^i\text{ with }y_i = 1 \\
w_0 + w_1x^i_1 + w_2x^i_2 \leq -1, \forall x^i\text{ with }y_i = -1 \\
$$
A slightly succinct form of writing this is,
$$
\min \|w\|_2 \\
\text{subject to} : y_i(w_0 + w_1x^i_1 + w_2x^i_2) \geq 1, \forall i
$$
This is basically the basic SVM formulation. I have skipped quite a lot of discussion for brevity. Hopefully, I still got most of the idea through.
CVX script to solve the example problem:
A = [1 2 1; 3 2 1; 2 3 1; 3 3 1; 1 1 1; 2 0 1; 2 1 1; 3 1 1];
b = ones(8, 1);
y = [-1; -1; -1; -1; 1; 1; 1; 1];
Y = repmat(y, 1, 3);
cvx_begin
variable w(3)
minimize norm(w)
subject to
(Y.*A)*w >= b
cvx_end
Addendum - Geometric Margin
Above we have already requested that we look for $w$ such that $y_i(w_0 + w_1x_1 + w_2x_2) \geq 1$ or generally $y_i(w_0 + w^Tx) \geq 1$. The LHS here that you see is called the functional margin, so what we have requested here is that the functional margin be $\geq 1$. Now, we will try to compute the geometric margin given this functional margin requirement.
What is geometric margin?
Geometric margin is the shortest distance between points in the positive examples and points in the negative examples. Now, the points that have the shortest distance as required above can have functional margin greater than equal to 1. However, let us consider the extreme case, when they are closest to the hyperplane that is, functional margin for the shortest points are exactly equal to 1. Let $x_+$ be the point on the positive example be a point such that $w^Tx_+ + w_0 = 1$ and $x_-$ be the point on the negative example be a point such that $w^Tx_- + w_0 = -1$. Now, the distance between $x_+$ and $x_-$ will be the shortest when $x_+ - x_-$ is perpendicular to the hyperplane.
Now, with all the above information we will try to find $\|x_+ - x_-\|_2$ which is the geometric margin.
$$w^Tx_+ + w_0 = 1$$
$$w^Tx_- + w_0 = -1$$
$$w^T(x_+ - x_-) = 2$$
$$|w^T(x_+ - x_-)| = 2$$
$$\|w\|_2\|x_+ - x_-\|_2 = 2$$
$$\|x_+ - x_-\|_2 = \frac{2}{\|w\|_2}$$
[1] It doesn't actually matter which side you choose for $1$ and $-1$. You just have to stay consistent with whatever you choose.