4
  • A property of the Maximum Likelihood Estimator is, that it asymptotically follows a normal distribution if the solution is unique.
  • In case of a continuous Uniform distribution the Maximum Likelihood Estimator for the upperbound is given through the maximum of the sample $X_i$.

I have a hard time figuring out how the distribution of the maximum converges in distribution to a Gaussian.

In the following Question it is claimed that the maximum of the sample $X_i$ of a $U[0,\theta]$ , with $\theta$ = 1, will follow a Beta distribution. Question about asymptotic distribution of the maximum

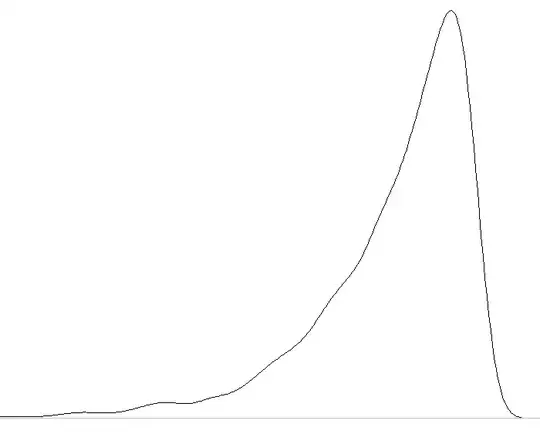
I also tried to figure it out empirically and always came to a more or less the result in the Graph bellow. Also from a logical point of view (atleast my logic) the distribution should never be able to converge to a Gaussian since the Expected Value of $\hat\theta$ is asymptotically equal to $\theta$ and because all possible $X_i$ have to be smaller than $\theta$, therefore there can not exist Values on the right side of $E[\hat\theta]$, which makes it impossible to converge to a Normal Distribution.

Where do I make my mistake? I haven't found a similiar question considering the contradiction.

enter image description here enter image description here

Mauro Schläpfer
  • 43
  • 6
  • 1
    Your first bullet item is not universally true. Check out the assumptions needed to prove it and see which one(s) do not hold in your case. (I cannot tell you the answer because your term "uniform distribution" is ambiguous. It appears you might mean the family of uniform distributions on the intervals $[0,\theta],\theta\gt 0.$) – whuber Nov 12 '19 at 21:51
  • A edited my question, the assumptions needed are that it has to have a unique solution. (Otherwise my script might be wrong / not complete) – Mauro Schläpfer Nov 12 '19 at 22:00
  • 3
    You have included *conclusions* but you haven't stipulated all the assumptions on which they rely. To see what can go wrong, suppose there are only two possible underlying distributions identified by parameter values $\theta\in\{0,1\}.$ Since the estimator will therefore be a value in $\{0,1\},$ there's no way it possibly could be asymptotically Normal, contradicting the highlighted bullet in the quoted text. As another example, consider estimating the mean of a Normal$(\mu,1)$ distribution where $0\le\mu.$ When $\mu=0,$ there's a 50% chance the MLE will equal $0:$ what happens asymptotically? – whuber Nov 12 '19 at 22:07
  • What are you referring to when you say the maximum likelihood of a uniform distribution on [0,1]. You need to be referring to a parameter of the distribution. Is it the mean, the standard deviation or something else? By the way the maximum of a random sample of size n from a uniform distribution can be normalized to converge to one of the 3 extreme value distribution types. They are not Gaussian distributions. – Michael R. Chernick Nov 12 '19 at 22:09
  • @MichaelChernick You are right, I should have stated that $\theta$ is the upper bound of the uniform distribution. – Mauro Schläpfer Nov 12 '19 at 22:17
  • @whuber Thanks for the answer and the example. I understand that $\hat\theta$ doesn't follow a Gaussian but that is only the case if the solution is not unique and I struggle to understand why it isn't unique in your comment. I mean $E[\hat\theta]$ is unique?! – Mauro Schläpfer Nov 12 '19 at 22:22
  • The maximum likelihood estimator of the parameter $\theta$ for that uniform distribution is the sample maximum. The sample maximum in this case is a biased estimate that converges to the true value of $\theta$. It does not converge to a non-trivial distribution. The solution is unique but cannot be normalized to converge to a Gaussian distribution. It can be normalized to an extreme value distribution. – Michael R. Chernick Nov 12 '19 at 22:30
  • 2
    Re "only the case:" that's not so. To conclude asymptotic Normality, one uses a version of the Central Limit Theorem. This requires so-called "regularity" conditions required to make the log likelihood look like a sum of iid random variables. These conditions typically require (1) all distributions have common support (ruling out your example); (2) the true parameter is in the interior of an open interval of possible parameters (ruling out my examples); (3) the Fisher Information is positive-definite; and (4) the likelihood is sufficiently highly differentiable to apply Calculus. – whuber Nov 12 '19 at 22:54
  • 3
    @Mauro Can you please edit your question to incorporate the corrections required (e.g. things like what you say in comments that you "should have said") – Glen_b Nov 12 '19 at 22:55
  • 1
    @whuber Thanks a lot! So the statement in the script is not sufficient, because the regularity conditions also have to be fullfilled. – Mauro Schläpfer Nov 13 '19 at 07:17

1 Answers1

8

A property of the Maximum Likelihood Estimator is, that it asymptotically follows a normal distribution if the solution is unique.

Not necessarily. So far as I am aware, all the theorems establishing the asymptotic normality of the MLE require the satisfaction of some "regularity conditions" in addition to uniqueness. Roughly speaking, these regularity conditions require that the MLE was obtained as a stationary point of the likelihood function (not at a boundary point), and that the derivatives of the likelihood function at this point exist up to a sufficiently large order that you can take a reasonable Taylor approximation to it. (The proofs of asymptotic normality then use the Taylor expansion and show that the higher order terms vanish asymptotically.)

The notes you have shown in your question gloss over this requirement, so I imagine that your teacher is interested in giving you the properties for the general case, without dealing with tricky cases where the "regularity conditions" do not hold. However, if you have a look at textbooks that actually prove the asymptotic normality of the MLE, you will see that the proof always hinges on these regularity conditions. (And indeed, good textbooks will usually supply counter-examples that show that asymptotic normality does not hold for some examples that don't obey the regularity conditions; e.g., the MLE of the uniform distribution.)

In the case of the MLE of the uniform distribution, the MLE occurs at a "boundary point" of the likelihood function, so the "regularity conditions" required for theorems asserting asymptotic normality do not hold. So far as I am aware, the MLE does not converge in distribution to the normal in this case.

Ben
  • 91,027
  • 3
  • 150
  • 376
  • +1. But in this example $\hat\theta$ is not at a boundary point: the likelihood function is defined on $(0,\infty)$ and almost surely $\hat\theta$ is nonzero. The assumption that fails here is that the distributions in the family must have common support. Since they don't, we obtain "extra" information from the data: namely, each value $x_i$ definitively rules out the possibility that $\theta \lt x_i.$ Some consequences are (1) convergence is faster than $O(n^{-1/2})$ and (2) the standardized asymptotic distribution of $\hat\theta$ is non-normal. – whuber Nov 13 '19 at 13:29
  • I guess it depends on what you mean as a "boundary point". In this context, I took this to mean the boundaries of the set of nonzero values of the likelihood function. Unless I'm mistaken, the likelihood is $L_\mathbf{x}(\theta) = \theta^{-n} \cdot \mathbb{I}(\theta \geqslant x_{(n)})$, so the MLE $\hat{\theta} = x_{(n)}$ does occur at a boundary point that is not a critical point of the function. – Ben Nov 13 '19 at 13:49
  • Because that's not the usual meaning of a "boundary point" of a function, I felt it would be useful to provide a clarifying comment. Note, too, that $x_{n}$ *is* a critical point according to the standard definition: https://en.wikipedia.org/wiki/Critical_point_(mathematics). However, similar examples occur (for the same underlying reasons) even where the likelihood function is infinitely differentiable. The three-parameter Lognormal family provides a good example. – whuber Nov 13 '19 at 14:09
  • Sorry, I meant to say it is not a "stationary point" (edited post to clarify) since the derivative does not exist at this point. – Ben Nov 13 '19 at 21:27