0

I have two classification models, $C_1$ and $C_2$, and I want to do a hypothesis test to see if $C_1$ is significantly better than $C_2$. I am interested in a one-sided hypothesis test. Thus I have the following hypotheses:

$H_0: \epsilon_1 = \epsilon_2$

$H_1: \epsilon_1 < \epsilon_2$

where $\epsilon_i$ are the respective error rates. I have $n$ samples from a validation set that I want to use to either accept $H_0$ or reject $H_0$. One choice for a hypothesis test that seems appropiate in this setting is the McNemar exact conditional test (I choose it because its easy to analyze and implement). I have implemented the test myself, and I'm checking to see if my implementation is correct.

Now I understand that if the $H_0$ is true, the distribution of the p-values should be uniform if the test statistical is continuous (see this question). Clearly the exact conditional test is discrete, but still, I would expect at least a sort of uniform histogram if $H_0$ is true (otherwise how can we guarantee a FPR bounded by the confidence level alpha?).

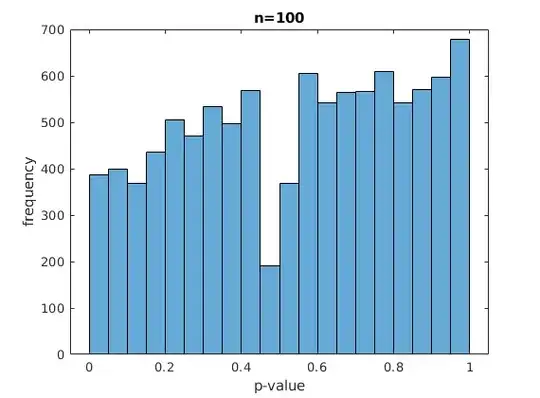
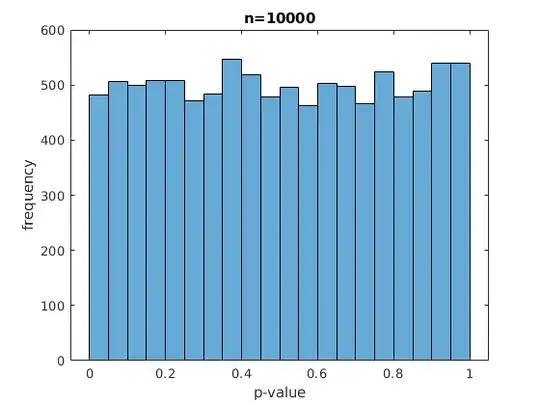
I have implemented the test, and performed two experiments. I set $\epsilon_1 = \epsilon_2 = \frac{1}{2}$, by simply making each classifier output a random coin flip, and all labels are random coin flips as well. I use either $n=100$ or $n = 10000$ for the size of the validation set. I simulate the experiment 10000 times. I observe the following histograms for the p-values:

enter image description here enter image description here

So for small values of $n$ the distribution looks really skewed. Can we conclude that there is something wrong with my implementation of the hypothesis test, or is this to be expected due to discretization? I would assume that if the discretization is the problem, the distribution would still more or less look uniform, and not become skewed. I repeated the experiment several times and the results seem consistently skewed for small $n$.

It seems someone had a related issue. This is why I'm no also looking at the empirical CDF of the p-values. This seems a bit more well-behaved, see below the empirical CDF for $n=100$:

enter image description here

Tom
  • 1,012
  • 6
  • 13
  • You state 'I want to do a hypothesis test to see if C1 is significantly better than C2' You cannot test this hypothesis using the McNemar test. The McNemar test measures whether disagreement between two tests is skewed towards when one is positive or the other is positive. At no point can it account for any measure of whether one is better or not. – ReneBt Nov 08 '19 at 14:35
  • Sorry, maybe I wasn't clear. But I have the outcome for each sample in the validation set that indicates whether $C_1$ is correct/incorrect and $C_2$ is correct/incorrect for that sample. Thus I construct a contingency table with: #C1 and C2 agree and correct, #C1 correct and C2 incorrect, #C1 incorrect and C2 correct, #both incorrect. Then McNemar can in my understanding be used to judge whether this difference is significant. See also https://arxiv.org/pdf/1811.12808.pdf section 4.3-4.4. – Tom Nov 08 '19 at 14:50
  • @ReneBt, I would say McNemar can be used to address one interpretation of "is better than". If you consider two processes where, on the same subject, either processes can succeed or fail. If the count of when process 1 succeeds in cases where process 1 fails, is greater than the count of when process 2 succeeds in cases where process 1 fails, then process 1 is "better". I've seen McNemar / Cochran Q used like this: "item is more popular", "test question is more difficult". That being said, this does appear to reflect the H1 of the question, but I don't quite understand the question. – Sal Mangiafico Nov 08 '19 at 15:02
  • The McNemars test as used in Tom's comment simply tests whether there is a skew between the two tests. There are appropriate tests for testing if one test is better, they take into account agreed mistakes. Because McNemar's does not include agreements it CANNOT test for 'betterness'. There is temptation to use McNemar's because it can give 'significance' at lower levels of difference, but implications are widely misunderstood. @sal-mangiafico you can see my full thoughts on what you suggest at https://www.researchgate.net/post/How_to_use_McNemars_test_to_compare_accuracy_of_classifications – ReneBt Nov 09 '19 at 11:31

0 Answers0