1

[Edit] I am working in R.

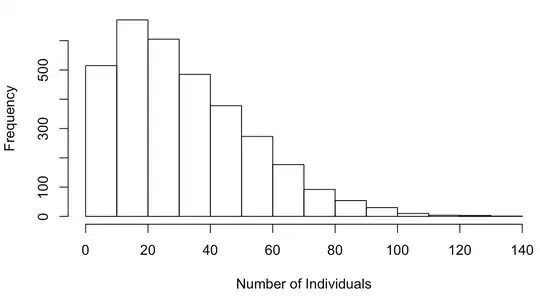
I am investigating the effects of weather on restaurant demand. My DV is the number of restaurant visitors per hour, my IVs are five weather variables and all other variables are control variables. Below you can find a frequency plot of my DV:

Histogram of data

After finding out that a multiple regression does not suit my data (i.e. my DV is a non-negative, discrete count variable), I decided to proceed with Poisson GLM. The code (simplified) is as follows: 

    glm(formula = Visitors ~ Temperature + Temperature_Squared + Pressure 
+ Clouds + Sun + Rain + Day_Fri + Day_Sat + Day_Sun + Day_Mon 
+ Day_Tue + Day_Wed + Hour_00 + Hour_01 + Hour_02 + Hour_13 
+ Hour_14 + Hour_15 + Hour_16 + Hour_17 + Hour_18 + Hour_19 
+ Hour_20 + Hour_21 + Hour_22 + Hour_23 + Holiday, family = "poisson" , data=dat)

I ran a dispersion test, returning the following results: enter image description here

  1. Although the dispersiontest is significant (= overdispersion), the alpha is close to zero (zero = equidispersion). What does this imply for my next steps and model selection?

  2. I ran the same model as above with family = "quasipoisson"and then ran the comparison as proposed by Tom Wenseleers here: pchisq(summary(poisson)$dispersion * quasipoisson$df.residual, quasipoisson1$df.residual, lower = F). This returns 0.4967107. How do I interpret this value? Is my Poisson or QuasiPoisson model better?

  3. I am also considering a Negative Binomial model. However, looking at the typical distribution of such models online (high frequency of low counts and extremely long tail), it does not seem to align with my data as provided in the frequency plot above. Can (should) I still proceed with this?

As you can see, I am pretty puzzled by all models, how to compare them and which one to pick. Hopefully, you can help me sort things out.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
Daniël Lutjens
  • 131
  • 1
  • 3
  • What about estimating all three models, look at the predictions they give, how different are they? Use cross-validations to see which model works better. – kjetil b halvorsen Dec 27 '19 at 17:29
  • Similar Q: https://stats.stackexchange.com/questions/413312/how-to-choose-best-multiple-regression-model-poisson-quasipoisson-negative-bino – kjetil b halvorsen Dec 27 '19 at 17:40
  • 2
    It appears that you have close to 2000 observations; with that many, it's easy to distinguish between, say, a.Poisson (20) and a Poisson(22.7). I would also expect an interaction between day of week and hour, and between week and weather... You might want to consider using splines for the time of day instead of discretizing. – jbowman Dec 28 '19 at 04:38

0 Answers0