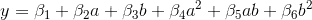1

Can someone help me to find the right time series model. I am not able to figure out the right hyper parameters for the model. Please see attached ACF and PACF graphs. I can provide more information if someone is willing to help.

I am using monthly data from 2013 to august 2019enter image description here

Link to the uploaded csv data http://www.sharecsv.com/s/7e254bfa6a0c8c44c357dc48e52a64fa/TimeSeries_Data.csv

Aditya Kamboj
  • 45
  • 4
  • 1
    Have you tried an automated model selection method, like `ets()` or `auto.arima()` in the `forecast` package for R? If not, why is manual model selection important to you? – Stephan Kolassa Nov 06 '19 at 09:22
  • Please find the uploaded csv. [link](http://www.sharecsv.com/s/7e254bfa6a0c8c44c357dc48e52a64fa/TimeSeries_Data.csv) - In the above example I was trying to forecast compact category. Yes, I have tried using Auto.Arima and ets in alteryx (R package) – Aditya Kamboj Nov 06 '19 at 17:16
  • you have 6 series each with 81 monthly values. The appropriate model for each series is likely to be similar with subtle differences between then . Pick one series ...the one that you are having the most trouble with and I will analyze that .. pursuing a potential hybrid model using both memory (arima) and latent deterministic structure. Please select one. – IrishStat Nov 06 '19 at 20:09
  • @ IrishStat , Thank you for your reply again sir. I think my pick would be Compact. I would love to understand the methodology and the thought process. Looking forward – Aditya Kamboj Nov 07 '19 at 17:04
  • I will try to accomplish that ... my post might be quite long as modelling is an iterative process much like peel an onion. – IrishStat Nov 07 '19 at 20:55

1 Answers1

0

There is nothing wrong whatsoever in using computerized aids as long as you understand the strengths and the shortcomings. Building a model is much like washing both sides of your face .. one needs to deal with both potential auto-projective (memory/arima) structure and deterministic structure ( pulses, level shifts , seasonal pulses and local time trends ). The approaches you have been investigating only deal with memory and are often flawed with over-parameterization and resultant statistical non-significance.

I have looked at your 7 series and perhaps the least complicated/thorough model formulation is the one you selected ...compact car sales over 81 periods . For pedagogical reasons I would have selected a more "difficult" series but life is short and I have analyzed the one you selected.

I will present the results of AUTOBOX's ( a piece of software that I have helped to develop ) and show critical results ...and then in a second phase actually try and unveil the logic behind the steps.

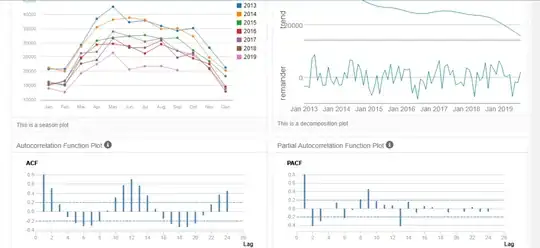
Initially the acf of the original series is here enter image description here clearly suggesting strong seasonal auto-regressive structure akin to the classic airline series of Box and Jenkins. The suggested model is (2,0,0)(1,0,0) a quite simple model in thew span of possibilities. I can't imagine why even band-limited procedures wouldn't deliver a similar model because the identified anomalies are VERY small BUT highly significant.

The Iterative modelling process https://autobox.com/pdfs/ARIMA%20FLOW%20CHART.pdf evolved to the following potentially useful model .

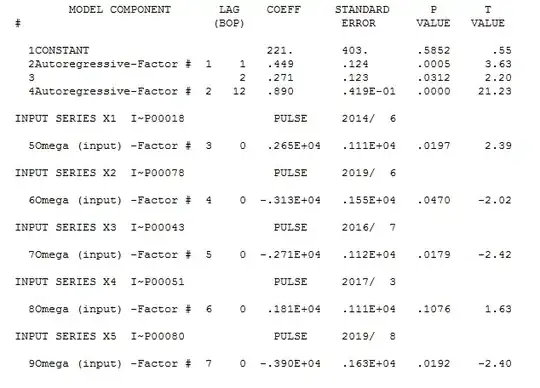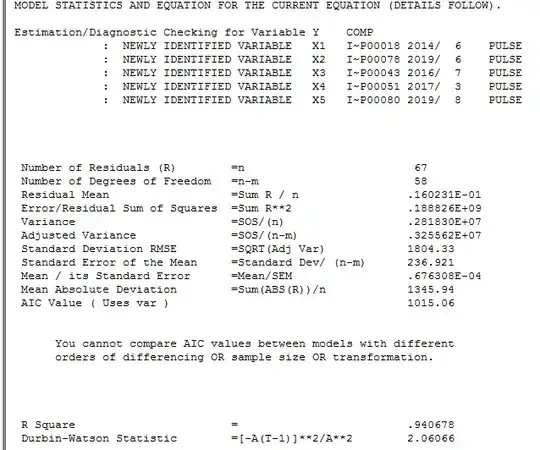enter image description here and here in more detail enter image description here withenter image description heremodel statistics here enter image description here

The Actual/Fit and Forecast is here enter image description here with monte-carlo driven re-sampling prediction limits for the next 36 periods .

The model residuals are here 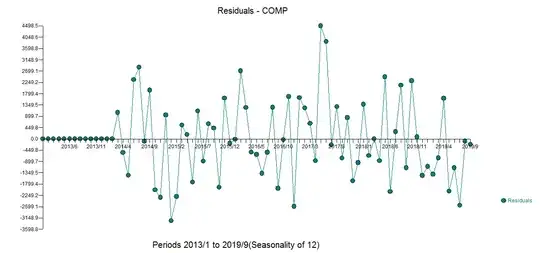enter image description here with an ACF here enter image description here

The forecasts are here enter image description here

The Actual and Cleansed graph is helpful to visually sipport the identification of the anomolous data points 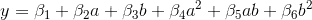enter image description here

I will now take a deep breath and attempt to detail the steps as you indicated that is what you really want.

STEP 1 : examine possible models following two mutually exclusive and distinctive paths ... Path 1 .. investigate possible arima models using a superset of the aic/bic ... auto.arima approach and for each possible prospect identify and incorporate additional deterministic structure that is statistically significant THEN take Path2 which identified deterministic structure and then incorporates/adds any evidented arima structure..... Select the most promising path penalizing models for excessive parameters

Note that models of the form 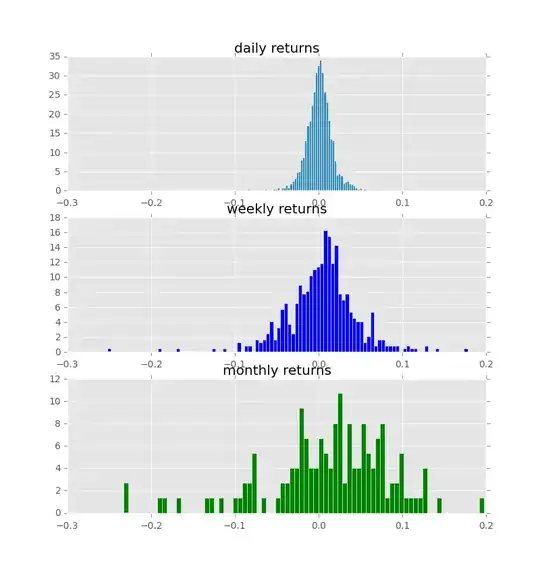enter image description here are also considered as a wide search is made for an equation that is as good as the human eye or at least similar as possible.

In this case the best model had an a seasonal ar(12) and a 2 parameter ar polynomial

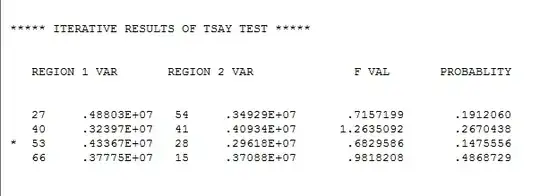
enter image description here

STEP 2 possible deterministic structure via the Tsay procedure http://docplayer.net/12080848-Outliers-level-shifts-and-variance-changes-in-time-series.html

enter image description here

enter image description here

Continuing we test for constancy of error variance over time .. suggesting constant error variance over time ( one of the Gaussian assumptions ignored by others ! ) Note that some of your other automotive series series required this GLS OPTION .

enter image description here

enter image description here

We now more closely examine the need for just pulses ....and obtain

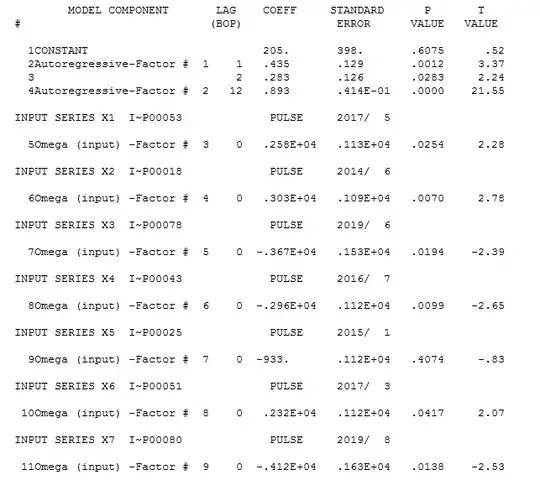
enter image description here

stepping down ( always a good idea ! ) we get

enter image description here

In terms of why your current approaches are failing , I can only suggest that you closely read @Adamo's wise reflections

"The correlogram should be calculated from residuals using a model that controls for intervention administration, otherwise the intervention effects are taken to be Gaussian noise, underestimating the actual autoregressive effect."

See @Adamo's response here

Interrupted Time Series Analysis - ARIMAX for High Frequency Biological Data?

IrishStat
  • 27,906
  • 5
  • 29
  • 55