The number of counts in a specific time period is modeled using a counting process with a deterministic or stochastic intensity. Stochastic process $N(t)$ is a counting process (point process) if
- $N(t)$ takes non-negative integer values,
- in each random scenario, the trajectory of $N(t)$ is piece-wise constant,
- in each random scenario, the trajectory of $N(t)$ is right-continuous,
- $N(t)$ is non-decreasing.
The intensity of counting process $N(t)$ is defined to be a stochastic process $\lambda(t)$ such that, for any time $t$ and shift $u$,
$$
P(N(t+u) - N(t) = 1 | N(s), 0 \leq s \leq t) = \lambda(t) u + o(u),
$$
where $o(u)$ is a function of $u$ which converges to $0$ when $u$ converges to $0$. The intensity stands for the expected number of jumps per unit of time in a very small time interval.
Counting process is a generalization of a non-homogeneous Poisson process. Non-homogeneous Poisson process jumps with a deterministic, time-varying intensity while counting process jumps with a stochastic, time-varying intensity (generally speaking). Typically, diffusion processes are used to model the intensity $\lambda(t)$. Ito diffusion is a stochastic process $X(t)$ satisfying the following stochastic differential equation:
$$
dX(t) = A(t,X(t)) dt + B(t,X(t)) dW(t),
$$
where $W(t)$ is Brownian motion.
In particular, if we choose to employ affine diffusions the counting process gains certain nice properties. In affine diffusions, $A(t,X(t))$ and $B(t,X(t))^2$ can be written as linear functions of $X(t)$.
This approach is the industry standard in actuarial science, derivatives pricing and survival analysis. If you have seen some simpler models, the chances are they fall within the aforementioned framework as special cases.
NOTES (addressing the follow-up questions):
1] $o(u)$ stands for "small o". The term is part of calculus. By definition, function $g(u)$ is "small o" with respect to function $f(u)$ when $u$ converges to $a$ if $g(u) / f(u)$ converges to 0 when $u$ converges to $a$.
2] Modeling jump intensity $\lambda(t)$ as a deterministic or stochastic process is a big field. Many methods and modeling ideas are part of it. $\lambda(t)$ does not always have to be complex but, in the presence of substantial amount of data, a clever diffusion-based model may improve the goodness of fit... To get acquainted with the field, please refer to the following references:
Duffie, D., & Singleton, K. (2003). Credit Risk: Pricing, Measurement, and Management. Princeton University Press.
Rausand, M. & Høyland, A. (2004). System Reliability Theory: Models, Statistical Methods, and Applications. Wiley-Interscience, Hoboken, New Jersey.
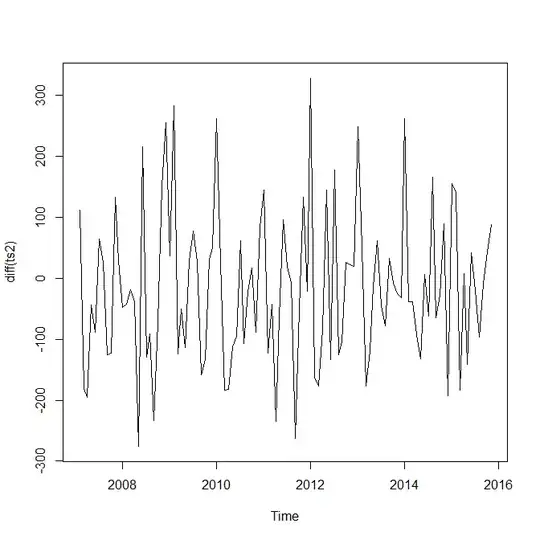
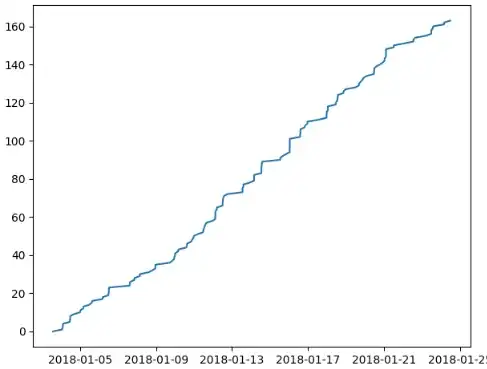So far, I've tried a linear regression algorithm, but proved to not be very accurate, likely due to the overall increasing trend. I also tried a neural net regression technique with a dataset consisting of the time until the end of the time period I'm predicting, the number of occurrences so far, and the total number of occurrences I am trying to predict, but it ended up just memorizing the dataset and not actually learning anything. Any help much appreciated!
