Integrating with Metropolis-Hastings

Question

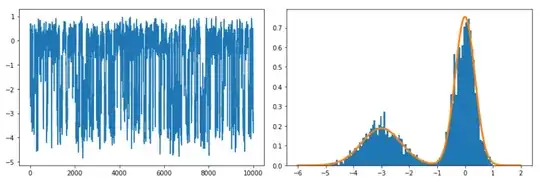
I am trying to implement a Metropolis routine to evaluate simple integrals. While it seem that the Markov chains I obtain reproduce the correct function, the area is simply wrong. Suppose I want to integrate the following (picture just below):

$$\int_{-5}^{1}2e^{4(-x^2)} + 0.5e^{-(x+3)^2}\text{d}x \approx 2.65$$

However, when I run my code I get a value of $\approx6.4$. I am not sure if this is due to my script or my choice of the prior interval (I assume it's $6$ from the uniform distribution within the bounds of integration).

This may be related to this issue, because I receive a similar incorrect value as in that post if I also run it for a sine function from $0$ to $\pi$, although I think I keep track of the rejected samples. I'm just learning the method so would appreciate simple answers.

def integrand(x):
    if -5. <= x <= 1.:
        return 2*np.exp(4*(-x**2)) + 0.5*np.exp(-(x+3)**2)
    else:
        return 0

n = 10000   #number of iterations

#performs algorithm and returns array of the samples 
def metropolis(f, iter=n):
    x = 0.   #initial x
    chain = np.zeros((iter, 1))

    for i in range(iter):
        x_new = np.array(x) + np.random.normal(size=1)
        if np.random.rand() < np.minimum(1, f(x_new) / f(x)):
            x = x_new
        chain[i] = x

    return chain

#run algorithm for the function
samples = metropolis(integrand, iter=n)

#evaluate area
area = 0
for i in range(len(samples)):
    area += function(samples[i])
area = 6*(1/len(samples))*area

print(area)

Xi'an · Accepted Answer · 2019-10-27T07:23:48.423

The code as given does not run since function is not defined. And the value of the integral is not 2.65.

Furthermore, even if we assume that function=integrand, there is a fundamental difficulty with the approach, namely that, if $$X_1,\ldots,X_n \sim f(x)$$ where $f$ is a density, then $$\frac{1}{n}\sum_{i=1}^n f(X_i)$$does not converge to $$\int f(x)\text{d}x$$ but to$$\int f^2(x)\text{d}x$$ Furthermore,

in the current case the density $f$ is known up to a constant $f=\mathfrak c \tilde f$. This does not invalidate the Metropolis-Hastings simulation of $$X_1,\ldots,X_n \sim f(x)$$but means that$$\frac{1}{n}\sum_{i=1}^n f(X_i)$$converges to $$\int \tilde f(x)f(x)\text{d}x$$
it is rarely possible to estimate the constant $\mathfrak c$ above from a simulation from $f$. Using importance sampling is a feasible alternative. For instance, using a Uniform sample on $(-5,1)$ works.

> 6*mean(2*exp(4*(-(u<-runif(1e6,-5,1))^2) + 0.5*exp(-(u+3)^2))) [1] 1.766225

> integrate(fun<-function(x)2*exp(4*(-x^2) + 0.5*exp(-(x+3)^2)),-5,1) 1.768901 with absolute error < 6.7e-10

Integrating with Metropolis-Hastings

1 Answers1