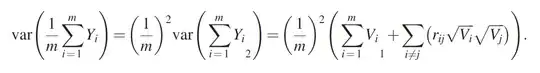I did multiple regression analysis.
There are 2 independence variables and one dependence variable.
Because there are heteroscedasticity problem, I did log transport about dependence variable.
All of the variable types are numeric.
""reg3<-lm(log(h3+1)~e3+i3,data=h3.train)"" (my code to fit the data)
I check the residual plots to see the model is well fitted.
I know the basic rules of interpreting residual plot in regression analysis.
But these 3 residual plots below are pretty ambiguous for me.
I want you to help me to interpret the plots and what should I do for next.
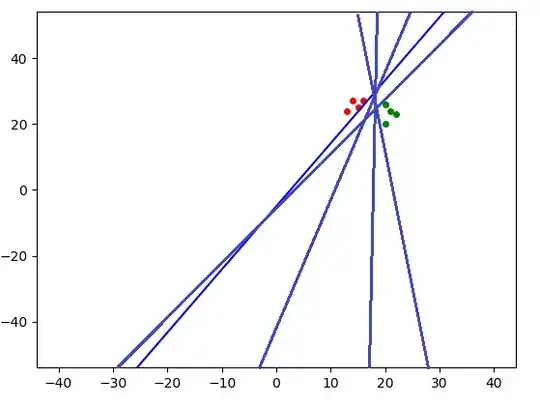
Here are the plots.
I think there some rules at the first graph.
I can see both small and big one line in the graph.
I don't think it is randomly distributed.
It looks the dots are randomly distributed.
But I can see there is a limit at the bottom line.
I mean at the under left. I can see there is a line.
I think this is ok. It seems that the residual spots are randomly distributed. But I doubt it could have same problem with the second graph. It is just difference of degrees.
Thank you for your help in advance. Sincerely.