Is there an upper limit on the number of intervals in a histogram?

Question

I've read several articles and excerpts from books that explain how to choose a good number of intervals (bins) for histogram of a data set, but I'm wondering if there's a hard maximum number of intervals based on the number of points in a data set, or some other criterion.

Background: The reason I'm asking is that I'm trying to write software based on a procedure from a research paper. One step in the procedure is to create several histograms from a data set, then choose the optimal resolution based on a characteristic function (defined by the authors of the paper). My problem is that the authors don't mention an upper bound for the number of intervals to test. (I have hundreds of datasets to analyze, and each one can have a different "optimal" number of bins. Also, it's important that the optimal number of bins is selected, so manually looking at the results and picking a good one won't work.)

Would simply setting the maximum number of intervals to be the number of points in the data set be a good guideline, or is there some other criterion that's typically used in statistics?

Answer 1

There really isn't any hard upper limit, but on the other hand, in most situations, once you get all unique observations in their own bin, finer bins only serve to pinpoint their positions more precisely without conveying much more. e.g. compare these:

Except in some very particular circumstances, there's likely to be no practical benefit in the second plot, and not that much in the first. If your data are continuous, this is probably way beyond a useful number of bins.

So in most situations, that seems like at least a practical upper bound - every unique observation in its own bin.

(If there is benefit in more bins than one per unique observation, you should probably be doing a rugplot or a jittered stripchart to get that kind of information) - something like what's done in the margins of these histograms:

(Those histograms are taken from this answer, near the end)

Answer 2

There is no hard maximum for the number of bins in a histogram. If the variable being plotted is continuous, then an argument can be made for an infinite number of categories (and the histogram basically becomes a rug plot).

The number of points in the data set is not an appropriate upper bound. Consider a data set containing two values: 1 and 1000. Having two bins would not be appropriate.

Two practical methods for determining an upper-bound are: a) Determining the underlying rounding of the data. For example, if the data is integers then it makes sense to have bins that are integer-width. b) Looking at the maximum visible resolution (e.g., number of pixels in the horizontal dimension that can be used for plotting).

Answer 3

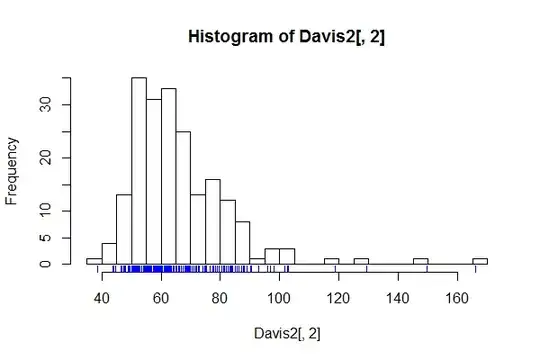
There is a good case for having a large number of bins, e.g. bins for every possible value, whenever it is suspected that the detail of a histogram would not be noise, but interesting or important fine structure.

This is not directly connected to the precise motivation for this question, wanting an automated rule for some optimum number of bins, but it is relevant to the question as a whole.

Let us leap immediately to examples. In demography rounding of reported ages is common, especially but not only in countries with limited literacy. What can happen is that many people do not know their exact date of birth, or there are social or personal reasons either for understating or for exaggerating their age. Military history is full of examples of people telling lies about their age either to avoid or to seek service in armed forces. Indeed many readers will know someone who is very coy or otherwise not quite truthful about their age, even if they do not lie about it to a census. The net result varies but as already implied is usually rounding, e.g. ages ending in 0 and 5 are much more common than ages one year less or more.

A similar phenomenon of digit preference is common even for quite different problems. With some old-fashioned measurement methods the last digit of a reported measurement has to be gauged by eye by interpolation between graduated marks. This was long standard in meteorology with mercury thermometers. It has been found that collectively some reported digits are more common than others and that individually many of us have signatures, a personal pattern of favouring some digits rather than others. The usual reference distribution here is the uniform, that is, as long as the range of possible measurements is many times greater than the "unit" of measurement, the final digits are expected to occur with equal frequency. So if reported shade temperatures could cover a range of (say) 50 $^\circ$C the ten last digits, fractions of a degree .0, .1, $\cdots$, .8, .9 should each occur with probability 0.1. The quality of this approximation should be good even for a more limited range.

Incidentally, looking at the last digits of reported data is a simple and good method of checking for fabricated data, one that is much easier to understand and less problematic than the currently fashionable scrutiny of first digits with an appeal to Benford's Law.

The upshot for histograms should now be clear. A spike-like presentation can serve to show, or more generally to check for, this kind of fine structure. Naturally, if nothing of interest is discernible, the graph may be of little use.

One example shows age heaping from the Ghana census for 1960. See http://www.stata.com/manuals13/rspikeplot.pdf

There was a good review of distributions of final digits in

Preece, D.A. 1981. Distributions of final digits in data. The Statistician 30: 31-60.

A note on terminology: some people write about the unique values of a variable when they would be better talking about the distinct values of a variable. Dictionaries and usage guides still advise that "unique" means occurring once only. Thus the distinct reported ages of a population could be, in years, 0, 1, 2, etc. but the great majority of those ages will not be unique to one person.