1

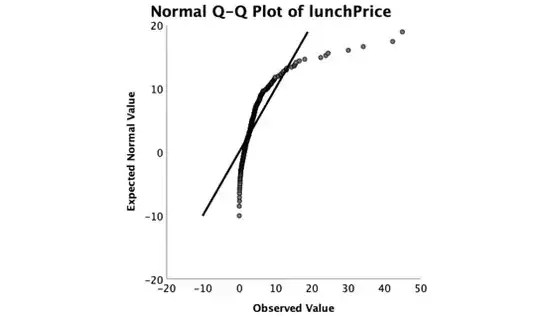
I'm doing stats and really struggling with what these plots tell me about my analysis! Just need to find out what these qq plots show me and what assumptions one can get out of them. Thanks all!

enter image description here

enter image description here

James Piner
  • 11
  • 1
  • 1
    What analysis are you performing? – whuber Oct 22 '19 at 18:00
  • 1
    Tastes vary: mine is to have the axes the other way round. Either way you have markedly positive skewed distributions a long way from normal. Your observed values all appear to be positive, no surprise for variables like income and price. Normal distributions with the same mean and SD would have many negative values. Similarly the upper tails of the data are fatter than the corresponding normal. In this case you aren't seeing much that would not also be evident in histograms with normal densities superimposed. The merits of quantile normal plots are greater with more subtle differences. – Nick Cox Oct 22 '19 at 18:02
  • 1
    See [this Q&A](https://stats.stackexchange.com/questions/101274/how-to-interpret-a-qq-plot) for more on qq-plots. – BruceET Oct 22 '19 at 18:37

1 Answers1

0

A qq plot is a plot of the quantiles from your data against the quantiles of a chosen probability distribution. A quantile is a fraction where the value of it represents the data value at which that fraction of data falls below the quantile. So for example the median is the 0.5 quantile and so it is the value at which 50% of the data are below it and 50% are above it.

So the premise behind the qq plot is that if a data set comes from a chosen theoretical distribution then you should get agreement between the theoretical distribution and the data set at each quantile. Agreement here means when you plot them against each other they make a straight line.

In your case they do not. So that tells you your data sets are not normally distributed. For example the normal distributions predict negative values while your data set doesn't have any (if you look at the left hand side of your plot).

Unrelated to your question: both of your variables (based on their name) are restricted to being positive and in that case it's usually recommended that you take the log of the data. I would try remaking those plots with a log transform.

References/Further reading:

https://www.itl.nist.gov/div898/handbook/eda/section3/qqplot.htm

https://data.library.virginia.edu/understanding-q-q-plots/

https://www.statisticshowto.datasciencecentral.com/q-q-plots/

Patrick
  • 1,369
  • 8
  • 14