Acceptance/rejection sampling and inverting CDF (R code illustration included)

Question

I have the following example:

Acceptance/rejection sampling

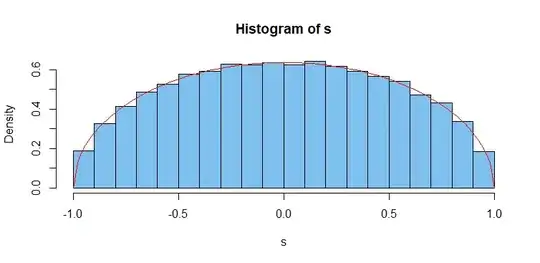
In some cases the cumulative distribution function might not be (easily) invertible. For example if $X$ has the probability density function: $$f_X(x) = \begin{cases} \dfrac{2}{\pi}\sqrt{1 - x^2} &\text{if } -1 \le x \le 1\\ 0&\text{otherwise}\end{cases}$$

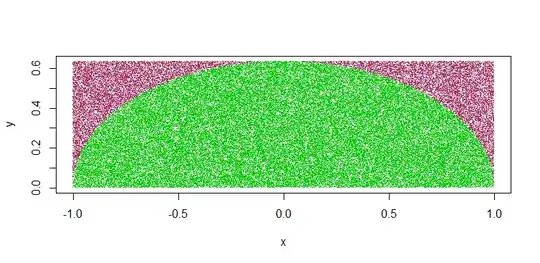
Which is the marginal distribution of $X$ if $(X, Y)$ are uniformly distributed on the unit circle. In this case we can use the following acceptance/rejection method:

Suppose that $f_X (x)$ is non-zero only on $[a, b]$ and $f_X (x) \le k$. Then we can simulate random variables from this distribution using the following approach:

1. Generate $x$ uniformly on $[a,b]$ and $y$ uniformly on $[0,k]$, $X$ and $Y$ independent of each other.
2. If $y < f_X (x)$ then return $x$, otherwise go back to step 1.

The following R code is provided to illustrate this example:

n <- 10000
x <- runif(n, min = -1, max = 1)
y <- runif(n, min = 0, max = 2/pi) 
ii <- y < 2/pi * sqrt(1 - x^2) 
sample <- x[ii]
length(sample)
## [1] 7873
hist(sample, prob = TRUE)
curve(2/pi * sqrt(1 - x^2), from = -1, to = 1, add = TRUE)

I'm wondering what the point of the case

2. If $y < f_X (x)$ then return $x$, otherwise go back to step 1.

is?

I don't understand where the $y$ is coming from, nor why, if $y < f_X (x)$, then we want to return $x$.

I would greatly appreciate it if people could please take the time to clarify this.

Answer 1

If this is supposed to be an exercise on the acceptance-rejection method, then I guess you're stuck with that, @Glen-b's excellent comment notwithstanding.

Your R code doesn't run as it stands. The 3rd line doesn't parse in R. It needs to be three separate statements--separated by line breaks or commas. If you fix that, I believe your code implements the method described.

I think the part with "otherwise go back" is pseudo-code and that you have taken care of it nicely in your R program (repaired as suggested).

Note: When presenting code (with answers that depend on calls to a pseudorandom number generator) for others to read, please consider putting a set.seed statement at the start for reproducibility.

When I ran my repaired version of your code letting R choose the seed, I got 7841 accepted values out of 10,000. (Starting with set.seed(1021), I got 7783.

Addendum: My version of R code with a few comments.

set.seed(2019)                       # for reproducibility
m = 10^5                             # nr of candidates
x = runif(m, -1,1)
y = runif(m, 0, 2/pi)
s = x[y < (2/pi)*sqrt(1-x^2)]        # accepted candidates
length(s)
[1] 78487                            # nr. accepted
hist(s, prob=T, col="skyblue2")
 curve((2/pi)*sqrt(1-x^2), -1,1, add=T, col="red")

summary(s); sd(s)
      Min.    1st Qu.     Median       Mean    3rd Qu.       Max. 
-0.9997643 -0.4028356  0.0009997  0.0011787  0.4052285  0.9992850 
[1] 0.4996049

Perhaps explanatory: accepted points in green.

plot(x,y, pch=".", col="maroon")
points(s,y[y< (2/pi)*sqrt(1-x^2)], pch=".", col="green3")

Answer 2

Ok, so I managed to gather the following:

We are not able to sample from $f_X (x)$ directly; instead, we sample $x$ from $\text{Unif}(a, b)$. However, in order to get the same values as sampling from $f_X (x)$, we must have a correction, and this is the purpose that $y$ serves. $x$, then, is a sample from $f_X (x)$. Now we can show that $X \le x$ and $Y \le f_X (x)$ would give the sample of $X$ from $f(x)$.