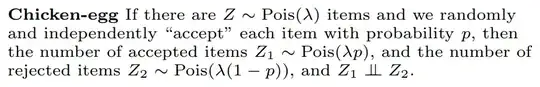In a probability cheatsheet, there's the following claim:
That $Z_1$ and $Z_2$ should be independent seems very unintuitive to me. It seems to me that if $Z_1$ is high, then $Z_2$ is low, and vice-versa. Is there an error in this cheatsheet, and if not, what is wrong with my intuition?
Given $Z$, $Z_1$ and $Z_2$ are not independent because $Z_1+Z_2=Z$, i.e. there is no conditional independence. But, if we also don't know $Z$, which factor enforces a relationship between $Z_1$ and $Z_2$? e.g. there is no force on $Z_2$ being low when $Z_1$ is high because we also don't know their sum.
Mathematically (let $z=z_1+z_2$), $$\begin{align}P(Z_1=z_1,Z_2=z_2)&=P(Z_1=z_1,Z=z)\\&=P(Z_1=z_1|Z=z)P(Z=z)\\&={z\choose z_1}p^{z_1}(1-p)^{z-z_1}e^{-\lambda}\lambda^z/z!\\&=\frac{1}{z_1!z_2!}(\lambda p)^{z_1}(\lambda(1-p)^{z_2})e^{-\lambda p}e^{-\lambda(1-p)}\\&=P(Z_1=z_1)P(Z_2=z_2)\end{align}$$
