I am looking for the distribution of a random variable $Z$ defined as
$$Z = \sqrt{X_1+\sqrt{X_2+\sqrt{X_3+\cdots}}} .$$
Here the $X_k$'s are i.i.d. and have same distribution as $X$.
1. Update
I am looking to find a simple distribution for $X_k$, that results in a simple distribution for the nested square root $Z$. Thus my idea to investigate distributions stable under some particular transformations. But this may not be the easiest way.
I tried a Bernoulli (with parameter $\frac{1}{2}$) for $X_k$, but this leads to some very difficult, nasty stuff, and a distribution on $[1, \frac{1+\sqrt{5}}{2}]$ full of gaps - some really big - for $Z$. So far the most promising result is the following.
Use a discrete distribution for $X_k$, taking on three possible values $0, 1, 2$ with the probabilities
- $P(X_k = 0) = p_1$
- $P(X_k = 1) = p_2$
- $P(X_k = 2) = p_3 = 1-p_1-p_2$.
Now the resulting domain for $Z$'s distribution is $[1, 2]$, and the gaps are eliminated. The resulting distribution is still very wild, unless $p_1, p_2, p_3$ are carefully chosen. Consider
- $p_1=\sqrt{5\sqrt{2}-1}-2$,
- $p_2=\sqrt{5\sqrt{3}-1}-\sqrt{5\sqrt{2}-1}$,
- $p_3=3-\sqrt{5\sqrt{3}-1}$.
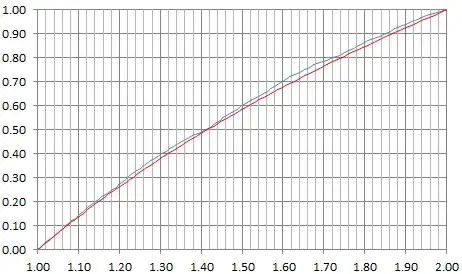
I was naively thinking that this would lead to $Z$ being uniform on $[1, 2]$, based on the table featured in my article Number Representation Systems Explained in One Picture (published here, see column labeled "nested square root", with row labeled "digits distribution".) But $Z$ does not appear to be uniform, though it does appear to be well behaved: it looks like $F_Z(z)$ is a polynomial of degree 2 if $z\in [1, 2]$. Then I modified a bit the values of $p_1, p_2, p_3$, removing 0.02 to $p_1$ and adding 0.02 to $p_3$. The result for $Z$ looks much closer to uniform on $[1, 2]$ this time.
Anyway, that's where I am now. My re-formulated question is: with appropriate values for $p_1, p_2, p_3$ (and what would these values be?) can we have a simple distribution for $Z$? (uniform or polynomial on $[1,2]$)
Note: With the particular discrete distribution in question, the support domain for $Z$ is $[1, 2]$. Sure, if all $X_k$ are zero, then $Z=0$ but that happens with probability zero. If all but one of the $X_k$ is zero, then $Z\geq 1$.
2. Second update
Regarding my statement I was naively thinking that this would lead to $Z$ being uniform on $[1, 2]$. I think the reason that it doesn't is because for this to happen, the $X_k$'s would need to have the right auto-correlation structure required to form a normal number in the numeration system based on infinite nested radicals. In my experiment, I used i.i.d. $X_k$'s. But for normal numbers (in that system) lag-1 auto-correlation between successive digits (the $X_k$'s being the digits) is close to zero, but not exactly zero. By contrast, in the binary numeration system, the digits $X_k$'s of normal numbers are not correlated, and thus if $X_k$ is Bernouilli of parameter $p=\frac{1}{2}$, then $Z = \sum_{k=0}^\infty X_k \cdot 2^{-k}$ is uniform on $[0, 1]$. But if $p\neq \frac{1}{2}$, then the distribution of $Z$ is pretty wild, see here.
3. Third update
Assume the $X_k$'s are i.i.d. with the discrete distribution mentioned earlier. Then the density $f$ associated with $Z$, if it exists, must satisfy:
$z \in ]1,\sqrt{2}[\Rightarrow f(z) = 2p_1 z f(z^2)$
$z \in ]\sqrt{2},\sqrt{3}[\Rightarrow f(z) = 2p_2 z f(z^2-1)$
$z \in ]\sqrt{3},2[\Rightarrow f(z) = 2p_3 z f(z^2-2)$
This excludes the possibility that $Z$'s distribution is as simple as a finite polynomial, regardless of $p_1, p_2, p_3$. Also, at $z=1, \sqrt{2}, \sqrt{3}$ or $2$, $f(z)$ may be zero, infinite, not exist or be discontinuous.
Finally, if $f(z)$ is properly defined (not zero or infinite) at $z=(1+\sqrt{5})/2$, then we have $p_2 = 1/(1+\sqrt{5})$: this is a direct result of the second equation in the above mathematical formula. Using the same equations with $z=\sqrt{2}$ and $z=\sqrt{3}$ yields $p_2/p_1=p_3/p_2$, if $f(1)$ and $f(2)$ are well defined. Combined with the value for $p_2$ and the fact that $p_1+p_2+p_3 =1$, we easily obtain interesting values: $p_1 = 1/2, p_2 = 1/(1+\sqrt{5}), p_3= (3-\sqrt{5})/4$. The following of this section is split into three cases.
Case 1:
If $p_1 = 1/2$ and $f(1)$ is well defined, one would assume that if $z \in ]1,\sqrt{2}[$ and the density is continuous, then $f(z) = f(1) / z$, because of the first formula resulting in
$$f(z) = f(\sqrt{z})/\sqrt{z} = f(z^{1/2^n})\cdot\Big(z^{\frac{1}{2}+\frac{1}{2^2}+\cdots +\frac{1}{2^n}}\Big)^{-1} \rightarrow \frac{f(1)}{z}.$$
Case 2:
The case $z\in ]\sqrt{2},\sqrt{3}[$ is quite interesting. Let's use $p_2 = 1/(1+\sqrt{5})$ and let $\phi = 2p_2$. Also, let us define $$R_1(z) =\sqrt{1+z}, R_2(z) =\sqrt{1+\sqrt{1+z}},R_3(z) =\sqrt{1+\sqrt{1+\sqrt{1+z}}}$$ and so on. Using the formula $f(z) = \phi\cdot\sqrt{1+z}\cdot f(\sqrt{1+z})$ iteratively, one gets $$f(z)=f(R_n(z))\cdot\phi^n\cdot\prod_{k=1}^n R_k(z).$$ The expression on the right-hand size converges as $n\rightarrow\infty$. Note that $R_n(z) \rightarrow \phi^{-1}$.
Note that if $z\in ]2^{1/4}, 3^{1/4}[$ then $f(z)$ can be computed either using case 1, or as follows: $f(z) = 2p_1 z f(z^2)$ and since $z^2 \in ]\sqrt{2}, \sqrt{3}[$ you can compute $f(z^2)$ using case 2. If the two different methods produce different results, the likely explanation is that $f(1)$ does not exist: $f$ oscillates infinity many times around $z=1$, making case 1 useless. This is something I have yet to explore.
Case 3:
Here $z\in ]\sqrt{3},2[$. I haven't checked it yet.