About the need of splitting data in stacking

Question

I learned stacking of machine learning in a book, hands-on machine learning 2nd edition (2019).

The picture was cited from hands-on machine learning 2nd edition (2019).

In the above situation, training set was split into 2 subsets. And the base predictors was trained on subset 1. Then the base predictors output values from the subset 2 and the blender was trained on this values.

My question is..
1. Why should the data used for training in the base predictors and the blender be different?

And the author said "Next, the first layer’s predictors are used to make predictions on the second (held-out) set (see Figure   7-14). This ensures that the predictions are “clean,” since the predictors never saw these instances during training."

2. What does 'clean' mean in this sentence?

I read a post of this link, but still i can't understand.

Answer 1

Why should the data used for training in the base predictors and the blender be different?

I think your confusion comes not from the explanation in the linked answer (which I think is great), but from the figures in the book. They display the flow of the data Below I've included my own version of them that display instead the task of the subset. Hopefully that helps clear this up:

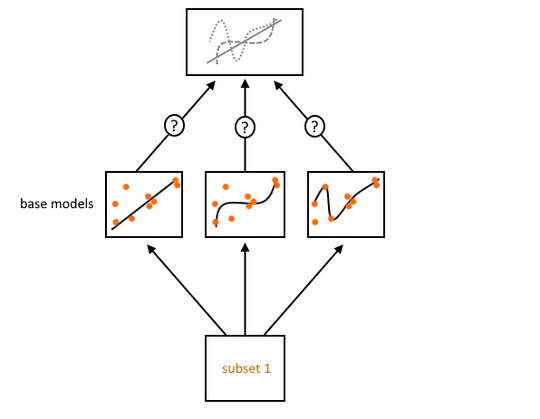
The purpose of $\color{darkorange}{\text{the first subset}}$ is used to train the base models separately. These then each make their own prediction. But how these models' predictions should be combined into a single overarching model (the "blender") has not been learned yet. Since you already trained these models on $\color{darkorange}{\text{subset 1}}$, reusing it is similar to re-training the base models on the same data: It causes them to overfit.

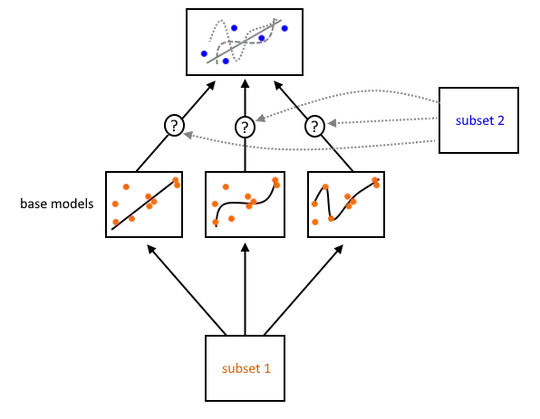
This is where $\color{blue}{\text{the second subset}}$ comes in: It learns the remaining problem of how to combine predictions from the base learners. These data have not been used to train the base learners, so any predictions from the base learners on $\color{blue}{\text{subset 2}}$ are "clean" in that the entirety of the training procedure has not seen them before.

Analogy: A Deep Neural Network

Can we not use the same data again to learn how to do that? It does not seem too dissimilar from how a multi-layer neural network has to learn the connections from the final hidden layer to the output layer... so what is the difference here?

Simple: Imagine that you would first freeze the connections leading up to the output layer. You train the other connections just until the model begins overfitting. You then unfreeze the output layer and freeze the rest instead. What happens? You begin overfitting, because the model has already been trained on the data to the extent that it can, without overfitting on the earlier part of the model. However, if you had had a subset 2 here, you could train this final layer without reusing anything.