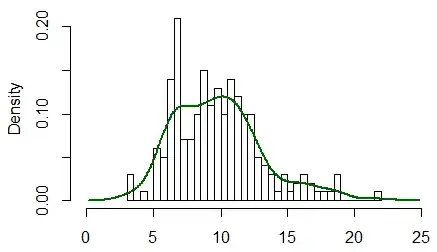
Are there 99 percentiles, or 100 percentiles? And are they groups of numbers, or dividers or pointers to individual numbers?

Question

Are there 99 percentiles, or 100 percentiles? And are they groups of numbers, or divider lines, or pointers to individual numbers?

I suppose the same question would apply for quartiles or any quantile.

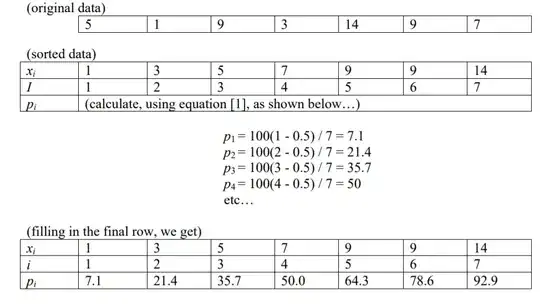
I have read that the index of a number at a particular percentile(p), given n items, is i = (p / 100) * n

That suggests to me that there are 100 percentiles.. because supposing you have 100 numbers(i=1 to i=100), then each would have an index(1 to 100).

If you had 200 numbers, there'd be 100 percentiles, but would each refer to a group of two numbers. Or 100 dividers excluding either the far left or far right divider 'cos otherwise you'd get 101 dividers. Or pointers to individual numbers so the first percentile would refer to the second number, (1/100)*200=2 And the hundredth percentile would refer to the 200th number (100/100)*200=200

I have sometimes heard of there being 99 percentiles though..

Google shows the oxford dictionary that says of percentile- "each of the 100 equal groups into which a population can be divided according to the distribution of values of a particular variable." and "each of the 99 intermediate values of a random variable which divide a frequency distribution into 100 such groups."

Wikipedia says "the 20th percentile is the value below which 20% of the observations may be found" But does it actually mean "the value below or equal to which, 20% of the observations may be found" i.e. "the value for which 20% of the values are <= to it". If it were just < and not <=, then By that reasoning, the 100th percentile would be the value below which 100% of the values may be found. I have heard that as an argument that there can be no 100th percentile, because you can't have a number where there are 100% of the numbers below it. But I think maybe that argument that you can't have a 100th percentile is incorrect and is based an error that the definition of a percentile involves <= not <. (or >= not >). So the hundredth percentile would be the final number and would be >= 100% of the numbers.

Answer 1

Both of these senses of percentile, quartile, and so on are in widespread use. It’s easiest to illustrate the difference with quartiles:

1. the “divider” sense — there are 3 quartiles, which are the values dividing the distribution (or sample) into 4 equal parts:

      1   2   3
   ---|---|---|---
   

   (Sometimes this is used with max and min values included, so there are 5 quartiles numbered 0–4; note this doesn’t conflict with the numbering above, it just extends it.)

2. the “bin” sense: there are 4 quartiles, the subsets into which those 3 values divide the distribution (or sample)

    1   2   3   4
   ---|---|---|---
   

Neither usage can reasonably be called “wrong”: both are used by many experienced practitioners, and both appear in plenty of authoritative sources (textbooks, technical dictionaries, and the like).

With quartiles, the sense being used is usually clear from context: speaking of a value in the third quartile can only be the “bin” sense, while speaking of all values below the third quartile most likely means the “divider” sense. With percentiles, the distinction is more often unclear, but it’s also not so significant for most purposes, since 1% of a distribution is so small — a narrow strip is approximately a line. Speaking of everyone above the 80th percentile might mean the top 20% or the top 19%, but in an informal context that’s not a major difference, and in rigorous work, the meaning needed should be presumably clarified by the rest of the context.

(Parts of this answer are adapted from https://math.stackexchange.com/questions/1419609/are-there-3-or-4-quartiles-99-or-100-percentiles, which also gives quotations + references.)

Answer 2

Take this answer with a grain of salt -- it started out fairly wrong and I am still deciding what to do with it.

The question is partly about language and usage, whereas this answer focuses on mathematics. I hope that the mathematics will provide a framework for understanding different usages.

One nice way to treat this is to start with simple math and work backwards to the more complicated case of real data. Let's start with PDF's, CDF's, and inverse CDF's (also known as quantile functions). The $x$th quantile of a distribution with pdf $f$ and cdf $F$ is $F^{-1}(x)$. Suppose the $z$th percentile is $F^{-1}(z/100)$. This provides a way to pin down the ambiguity you identify: we can look at situations where $F$ is 1) not invertible, 2) only invertible on a certain domain, or 3) invertible but its inverse never attains certain values.

Example of 1): I'll leave this for last; keep reading.

Example of 2): For a uniform 0,1 distribution, the CDF is invertible when restricted to [0, 1], so the 100th and 0th percentiles could be defined as $F^{-1}(1)$ and $F^{-1}(0)$ given that caveat. Otherwise, they are ill-defined since $F(-0.5)$ (for example) is also 0.

Another example of 2): For a uniform distribution on the two disjoint intervals from 0 to 1 and 2 to 3, the CDF looks like this.

Most quantiles of this distribution exist and are unique, but the median (50th percentile) is inherently ambiguous. In R, they go half-way: quantile(c(runif(100), runif(100) + 2), 0.5) returns about 1.5.

Example of 3): For a normal distribution, the 100th and 0th percentiles do not exist (or they "are" $\pm \infty$). This is because the normal CDF never attains 0 or 1.

Discussion of 1): For "nice" cdf's, such as with non-extreme quantiles or continuous distributions, the percentiles exist and are unique. But for a discrete distribution such as the Poisson distribution, my definition is ambiguous because for most $z/100$, there is no $y$ with $F(y) = z/100$. For a Poisson distribution with expectation 1, the CDF looks like this.

For the 60th percentile, R returns 1 (quantile(c(rpois(lambda = 1, n = 1000) ), 0.60)). For the 65th percentile, R also returns 1. You can think of this as drawing 100 observations, ranking them low to high, and returning the 60th or 65th item. If you do this, you will most often get 1.

When it comes to real data, all distributions are discrete. (The empirical CDF of runif(100) or np.random.random(100) has 100 increments clustered around 0.5.) But, rather than treating them as discrete, R's quantile function seems to treat them as samples from continuous distributions. For example, the median (the 50th percentile or 0.5 quantile) of the sample 3,4, 5, 6, 7, 8 is given as 5.5. If you draw 2n samples from a unif(3,8) distribution and take any number between the nth and (n+1)th sample, you will converge on 5.5 as n increases.

It's interesting to also consider the discrete uniform distribution with equal probability of hitting 3,4,5,6,7,8. (A die roll plus two.) If you take the sample-and-rank approach outlined above for the Poisson distribution, you will usually get 5 or 6. As the samples get bigger, the distribution for the number halfway up will converge on half fives and half sixes. 5.5 seems like a reasonable compromise here too.

Answer 3

I was taught that an observation in the nth percentile was greater than n% of observations in the dataset under consideration. Which to me implies that there is no 0th or 100th percentile. No observation can be greater than 100% of observations because it forms part of that 100% (and a similar logic applies in the case of 0).

Edit: For what it's worth, this is also consistent with non-academic usage of the term that I've encountered: "X is in the nth percentile" implies that the percentile is the group, not a boundary.

I unfortunately have no source for this that I can point you to.

Answer 4

There are other ways to calculate percentiles, what follows, is not the only one. Taken from this Source.

---

The meaning of percentile can be captured by stating that the $p$th percentile of a distribution is a number such that approximately $p$ percent ($p\%$) of the values in the distribution are equal to or less than that number. So, if $28$ is the $80$th percentile of a larger batch of numbers, $80$% of those numbers are less than or equal to $28$.

To calculate percentiles, sort the data so that $x_1$ is the smallest value, and $x_n$ is the largest,

with $n$ = total number of observations, $x_i$ is the $p_i$th percentile of the data set where:

$p_i = \dfrac{100(i - 0.5)}{n}$

Example from the same notes for illustration:

To take a single example, $7$ is the $50$th percentile of the distribution, and about half of the values in the distribution are equal to or less than $7$.

If you had 200 numbers, there'd be 100 percentiles, but would each refer to a group of two numbers.

No.

Assuming the numbers are sorted in ascending order moving from $x_1$ to $x_\mathrm{200}$. In this case the percentiles are:

$\dfrac{100(1-0.5)}{200}$, $\dfrac{100(2-0.5)}{200}$, $\dfrac{100(3-0.5)}{200}$, $...$

resulting in

$0.25, 0.75, 1.25 ... $ percentiles corresponding to indices $1, 2, 3, ...$

Answer 5

Note- I will accept somebody else's answer rather than mine. But I do see some useful comments so I'm just writing an answer that mentions those.

Based on Nick's answer "-iles" terminology for the top half a percent

it seems that the terms are ambiguous, and I suppose (based on my understanding of that post), better terminology would be X% point, and X%-Y% group; so quantile point(so for quartile points that could be anything from 0 to 4); quantile group ranging from X quantile point to Y quantile point.

Either way one would get 101 for percentiles, although one comment suggests that one could refer to 101 points (I suppose if you counted percentile points, and only integers), but even then, if one speaks of 1st, 2nd, 3rd, percentile or quantile, it's counting and one can't count the first as 0, and you can't have e.g. more than 4 quartiles or more than 100 percentiles. So if talking 1st, 2nd, 3rd, that terminology can't really refer to point 0. If somebody said 0th point, then while it's clear they mean point 0, I think they should really say quantile point 0. Or Quantile group at point 0. Even computer scientists wouldn't say 0th; even they count the first item as 1, and if they call it item 0, that's an indexing from 0, not a count.

A comment mentions "There can't be 100. Either 99 or 101, depending on whether you count maximum and minimum". I think there's a case for 99 or 101, when talking about quantile points rather than groups, though I wouldn't say 0th. For n items, An index may go from 0...n-1 and one wouldn't write th/st e.g. 1st, 2nd etc, on an index(unless perhaps the index happened to index the first item as 1). But an index starting the first item with index of 0 isn't a 1st, 2nd 3rd count. e.g. item with index of 0 is the 1st item, one wouldn't say 0th and label the second item 1st.