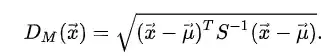I've read quite a few explanations on this topic, liking this one the most: https://mccormickml.com/2014/07/22/mahalanobis-distance/
But there is still one thing I don't understand.
I understand that the inverse of the covariance would deal with transformation of the (x-mu) to the standard gaussian. What I don't get is how is x^T infected by it?
To me, it seems that the we then take the dot product of elements 2 and 3 of the product, we transform only the (x-mu), and the first vector (x-mu)_transposed stays the same. So in the end we would get the dot product between the original vector and the transformed one.