t-test for a non-normal population

Question

Disclaimer: I'm a programmer. I am not a statistician. My last statistics class was (ermumble) years ago.

I read t-distibution for sample mean from non normal population and while I'm sure you all know exactly what you're talking about, I don't, so I'll ask for my specific case.

This is part of a class. The data set is (apparently) from Kaggle. The data is "medical charges". There are 1338 records. Naive statistics on the set give us:

mean: 13270.42 
std. dev.: 12110.01
median: 9382.03

and a histogram as shown:

Decidedly not a normal distribution.

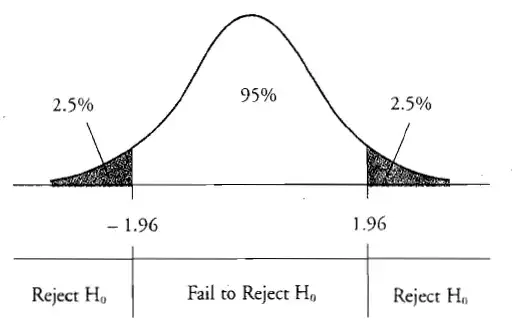
The class exercise asks: "The administrator is concerned that the actual average charge has fallen below 12000. On the assumption that these data represent a random sample of charges, how would you justify that these data allow you to answer that question? What would be the most appropriate frequentist test to apply? What is the appropriate confidence interval in this case? A one-sided or two-sided interval? Calculate the critical value and the relevant 95% confidence interval for the mean and comment on whether the administrator should be concerned?"

I figured, Central Limit Theorem, resample the means and work toward a better distribution.

m = medical.charges.to_numpy()

seed(47)
sample_mean = []

# calculate 100 means sampled from the larger dataset
for n in range(100):
    this_sample = np.random.choice(m, 50)
    sample_mean.append(np.mean(this_sample))

mean_of_means = np.mean(sample_mean)
std_of_means = np.std(sample_mean, ddof=1)

print("mean", mean_of_means, "\nstd. dev.:", std_of_means)

I ended up with a resampled mean of 13326 and a resampled
std. dev.: 1476 and plugged them into a t-test.

However apparently, the exercise expects me to simply plug the initial mean and std. dev into the t-test. (I know this because the following exercise tells me what answer they expected me to get for this one.)

Can I just blithely push the "mean" and "std dev" of this extremely non-normal data set through a t-test? And if so... why? (given that the docs all say "for a normal distribution...")

Answer 1

The solution shouldn't plug the standard deviation into the t-test, but if they used the standard error then that sounds more appropriate. Because you are not a statistician (and, dare I say, statistically savvy), I'll try to explain without any math.

The sample mean is just a scaled sum: Add up the data and divide by the number of data points. Because the sample mean is a sum, we can use the Central Limit Theorem to do inference about this sum.

The Central Limit Theorem says that when we have enough data, the sampling distribution of the sample mean is Normal with expectation equal to the population mean and standard deviation equal to the standard error.

Go ahead; plot your re sampled means. I bet they look normal. Check the standard deviation of those resamples. I bet it is close to the standard error.

The sample mean is thus a draw from this distribution. We can perform inference on it by subtracting the mean (in this case, the hypothesized population mean 12000) and dividing by the standard deviation (in this case, the standard error).

Because we don't know the standard deviation exactly, we have to estimate it. When we use an estimate of the standard deviation in our test, we switch from using a z-test to a t-test.

So, because the sample mean is assumed to come from a normal distribution (thanks to the Central Limit Theorem), we can use a t-test on this non-normal data.

If you can get your hands on "An Introduction to Medical Statistics" by Martin Bland, he does a very good job outlining this rationale in chapter 8.

Answer 2

The average of your sample of 1338 records is a single value, $\bar x$. That $\bar x$ is, itself, a member of a distribution of averages of all possible simple random samples of 1338 records. You don't have access to any other members of this distribution, so you can't plot it. You can't resample it. It's out there, somewhere, in the world, waiting for someone else to gather exactly 1338 records and take an average. You did that thing, and obtained a single observation from that distribution. Your $\bar x$.

Even though we only have one observation from that distribution (of all possible $\bar x$ from samples size 1338), with some minimal assumptions about the distribution of $x$ (individual records), we can figure out a whole lot from the single observation of $\bar x$ that we have.

Specifically, in relation to your question, we can compute the probability of having obtained a sample with that mean, (your actual, measured $\bar x$), if we hypothesize a potential mean for the whole population mean $\mu$.

Fortunately for you, someone else has made just such a hypothesis. Specifically, the administrator is concerned that the actual average charge has fallen below 12000. In other words, the administrator has hypothesized that "I hypothesize that the actual average is perhaps below 12000! We should gather evidence to test that hypothesis. SCIENCE!"

This means that we can compute the probability of obtaining something as large as our measurement of $\bar x$ or larger in the event that the actual average actually were less than 12000. If this probability is low, then our $\bar x$ provides some evidence that the actual average is not, in fact, less than 12000 (because, if it were, then how did we obtain this totally improbable $\bar x$?)

That probability is $p$ from your t-test. Note that your sample distribution doesn't factor into it. The central limit theorem comes into play when one wants to prove that the t-test works for situations like this. If you're not writing a proof, then you don't really need to use it.

If you are curious as to just how close to a normal distribution the distribution of the sample mean is:

This is a beta distribution with $\alpha=\beta=0.1$

It's pretty not normal. It's about the opposite of normal. But let's suppose that our population is distributed this way.

If we plot the distributions of the sum of a simple random sample of $n$ observations from our population distribution (not to scale):

Even for a sample as small as 16, the results are looking pretty normal-ish. Of course, we're usually trying to approximate the tails, so the shape of the middle there might be a little misleading, but this is converging really fast.