This article suggests we take this approach when attempting to conclude significant statistical difference between groups:
If this method is valid, is this the best approach when concluding statistical difference between groups? After looking at Bayesian approaches, my understanding is if you can assign a prior distribution with some backing (how would you do this?) then a Bayesian approach provides you with richer information, compared to a NHST.
The first question is whether you really want significance testing. I'm not sure you do, but, if you do, then, sure, the results of Bayesian analysis might give more information, if you supply more information to them by choosing an informative prior. But TANSTAAFL (there ain't no such thing as a free lunch). What if your prior is wrong? From what I have read (certainly not extensive) Bayesian results with a non-informative prior wind up similar to frequentist results.
Second, I'm always leery of diagrams like the one you present. They can be useful guides and they are helpful for beginners, but there are always exceptions and special cases.
Third, your title question. Are there better methods than NHST? Well "better" isn't defined, but for most purposes, I'd say "yes". I once attended a lecture by Patricia Cohen who, in addition to being a statistician was the widow of Jacob Cohen. She told us that he had wanted to label the method that is usually called null hypothesis significance testing (NHST) something else instead: Statistical Hypothesis Inference Testing (acronym here).
How big is the difference? How precise is our estimate of that difference? How is the variable distributed in each group? Might the difference be much larger or smaller than our estimate?
Those are usually more interesting questions than "is this difference significant?"
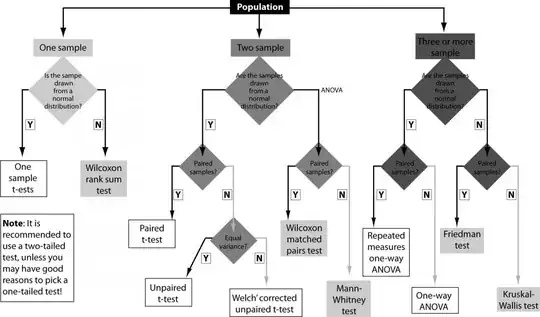
If this method is valid, is this the best approach when concluding statistical difference between groups?
The key word here is best.
Bayesian methods are best in a different way from Frequentist methods being best.
They are not solving the same problem. Using Keynesian notation, the user of a Frequentist method is answering $\Pr(data|\theta)$ while the user of a Bayesian method is answering $\Pr(\theta|data)$.
These are only superficially the same questions when the Frequentist null hypothesis is $\mu_1-\mu_2\ge{0}$. On top of this, the two methods, whether implicitly or explicitly are using different loss functions to accomplish their goals.
Frequentist methods, such as this, minimize the maximum possible risk of loss that you could experience. That is an incredibly positive thing if you lack prior information. The Bayesian method would minimize your average loss subject to your prior distribution.
That is a giant difference. If you have a real prior distribution, then that is the same thing as being able to put a problem in a context. It becomes quite reasonable to minimize the average loss. If your real prior is flat, it is like trying to solve a problem without a context to understand a loss in. Imagine trying to write fire insurance with no experience to think about loss in!
Frequentist methods are best in another way. Frequentist methods are a probabilistic form of modus tollens. It is a highly flawed almost equivalence but it closes the inference whereas Bayesian methods cannot.
Modus tollens is "If A, then B and Not B. Therefore, Not A." Translated into statistical talk, "if the null is true then the estimator will appear inside this region. It is not inside this region, therefore, subject to a level of confidence we can reject A as true.
Prior to Einstein, it was known that Mercury did not follow Newton's laws. Had a statistical test been performed, the Frequentist method would have rejected the null that Newton's laws were true. Bayesian methods can only test known hypotheses. Prior to Einstein, relativistic motion couldn't be formulated and so could not be tested in a Bayesian methodology. It could test many models but it couldn't test an idea that had yet to be conceived. It would, instead, grant probabilities to each potential model based on its closeness to reality. Bayesian methods can only test known ideas.
On the other hand, where a Bayesian method may have been valuable was in looking at which lines of thought were more likely to be true than others.
Finally, Frequentist methods are best when you need a fixed guarantee against false positives or a need to control the level of false negatives by controlling for power.
Now let's talk about the weaknesses of Frequentist methods.
First, they do not make direct probability statements. A p-value of less than five percent means that if the null hypothesis is true then there is less than a five percent chance of observing this outcome or something more extreme. That doesn't mean the null is false. It could just mean the sample is weird.
I do not remember who created this example, but this might help understand why rejecting the null may be a problem. There are 329 million people in the United States. You are walking down the street and encounter a member of Congress. The probability of encountering a member of Congress, subject to a handful of assumptions, is $\frac{435}{329717132}<.05$, therefore you can reject the null hypothesis that the person you encountered was an American.
Frequentist methods conflate "dang, that's weird," with "wow, that's false."
The second can be seen in the above null hypothesis. The Frequentist test would be a variant of using Student's t distribution. The Bayesian test, with a flat prior, would use the Behrens-Fisher distribution. The use of Student's t-distribution has nothing to do with the true probabilities involved but instead depends on a variety of modeling assumptions being true. If you would test it with the medians instead, you would use a different test distribution. The Bayesian distribution, on the other hand, is a probability distribution subject to the data and the prior.
If you used your real prior distribution, then you could safely place gambles of money using the Bayesian outcome but not the Frequentist one.
A third weakness is a loss of precision in exchange for an unbiased answer. Bayesian methods, in the presence of real information, can produce results that are far more precise than Frequentist ones. However, even with a flat prior, a Bayesian method will not, on average, have a higher squared loss than a Frequentist method. Bayesian methods make an automatic tradeoff between precision and accuracy. The preoccupation in many areas of Frequentist statistics for unbiasedness forces tradeoffs that a scientist might not make if they were forced to mentally walk through those tradeoffs as a conscious decision.
Frequentist methods are ex ante optimal in the sense that if you have yet to see your data and you have to choose an optimal procedure, regardless of what you end up with, then the Frequentist procedure will be that procedure.
Bayesian methods are ex post optimal. Given the data you actually encountered, if you needed to design an optimal procedure that will draw the highest amount of information out of it as is possible then you will use the Bayesian procedure.
EDIT If your question is regarding whether the chart could be improved, the answer is yes but you would really then be deriving all the variants and special cases that could happen but rarely do. There is also the problem that there may not be a unique solution to a particular problem. One thing notable about statistics is the absence of uniqueness theorems.
For example, for most normally distributed data, inference about the location of the parameter can be solved by using the sample mean and a t-test. However, consider a case where there are asymmetric losses with respect to your estimator. In other words, in solving $\hat{\theta}-\theta$, if the difference is negative you have a small loss but if it is positive you get a large loss.
An example of this could be robotic surgery where you need to avoid a nearby artery that is hidden under the tissue you are cutting. If you are to the left of the target you unnecessarily damage tissue but the effect is minor. If you are to the right of the artery you may damage the artery and kill the patient. An unbiased estimator may kill the patient fifty percent of the time. You do not want to use a sample mean as the consequences could be catastrophic.
Likewise, you want a conservative inference performed. Yes, you are going to be inaccurate more often than not but you won't kill the patient.
Your chart could have an infinite number of branches if you wanted it. You could also teach formal optimization as that is intrinsically more robust. Unfortunately, it is also too remote for most students to approach.
There almost never exists a unique way to do things in statistics!
You always need to define what you mean by best !
