The distribution is discrete rather than continuous, since the number of seats won is an integer in the range $[0, 151]$. The problem is that the information you have doesn't fully specify the distribution. Rather, it can be viewed as a set of constraints the distribution must satisfy (more on this below). So, how can we choose a distribution in this underspecified setting?
Principle of maximum entropy
A reasonable choice follows from the principle of maximum entropy. Loosely, it states that we should choose the distribution that's consistent with existing knowledge, and that that otherwise maximizes our uncertainty. Any other choice would either violate known facts or assume things we don't actually know. More formally, we consider the set of all distributions that satisfy a set of constraints representing our knowledge. From among this set, we choose the distribution with the greatest entropy, which measures uncertainty about the quantity the distribution is defined over. The result is called the MaxEnt distribution for short.
Defining the distribution
To formalize things, let $X$ be a random variable representing the number of seats won. We can represent the distribution of $X$ using a vector $p = [p_1, \dots, p_{152}]^T$, where $p_i$ represents the probability that $X=i-1$. So, the first element contains the probability of winning 0 seats, and the last element contains the probability of winning all 151 seats.
Defining constraints
You have information like "11.6313% chance of winning 71-75 seats". This can be translated to a constraint on $p$ as follows. The probability of winning 71-75 seats is given by the sum of elements 72-76 of $p$. This sum must equal .11631.
All constraints can be expressed simultaneously by the equation $C p = v$, where $C$ is a matrix with size $9 \times 152$ and $v$ is a vector with length $9$. Each constraint (of which you have 9) is represented by a row of $C$ and the corresponding element of $v$. $C$ contains a pattern of zeros and ones that specify how to take sums over $p$. $C_{ij} = 1$ if element $j$ of $p$ should be included in the sum for the $i$th constraint. $v_i$ contains the value that this sum must take. For example, the first row of $C$ should contain ones in columns 1-61, and the first element of $v$ should contain .00392. This represents the first constraint "0.3920% chance of winning 60 seats or fewer".
I'll assume these constraints represent the total available knowledge about the distribution.
Finding the MaxEnt distribution
The MaxEnt distribution is obtained by solving the following constrained optimization problem:
$$\max_p \ -\sum_i p_i \log(p_i) \quad \text{subject to:}$$
$$C p = v \quad \quad
p_i \ge 0 \ \forall i \quad \quad
\sum_i p_i = 1$$
The quantity being maximized is the entropy (where we define $0 \log(0) = 0$ to avoid undefined values). $C p = v$ represents the constraints described in the previous section. The final two constraints simply force the elements of $p$ to be nonnegative and sum to one, so that $p$ represents a valid probability distribution.
Result
It might be possible to solve the above optimization problem analytically. But, here's the result of solving it numerically, using a standard optimization algorithm:
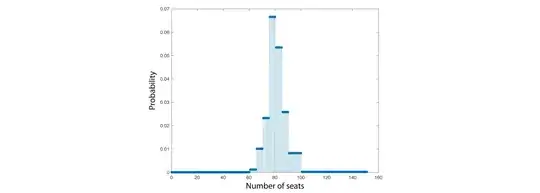
As you can see, the MaxEnt distribution is uniform on each of the intervals specified in the constraints. For example, the constraint "33.2789% chance of winning 76-80 seats" translates to 76,77,78,79, and 80 seats each having probability around .066 (given by dividing the total probability assigned to this range by the number of seats it contains).
This is exactly what one would expect, because no information has been given to distinguish the seats in each specified range. And, being maximally uncertain, we should treat them equally. This is a somewhat hand-wavy argument, but I think it should be possible to prove this formally, using the well-known fact that the discrete uniform distribution is the MaxEnt distribution on any finite set of values (in the absence of any further constraints).
Notes
The result is equivalent to what @PeterFlom suggested (+1). MaxEnt provides a justification for this choice: it's the distribution that's exactly consistent with the information provided, and is otherwise maximally uncertain (i.e. no further assumptions are made). It also gives a principled framework for solving this type of problem in general. If available, additional information and assumptions could be encoded as constraints in the MaxEnt problem, as shown below.
Imposing further assumptions
Here's an example showing how some further assumptions could be incorporated into the problem. These are not specified in the original question, but might be considered reasonable things to expect.
The distribution is unimodal. That is, probability assigned to each number of seats decreases monotonically as we move away from the peak. This is encoded as another set of constraints: $B p \le \vec{0}$ (where $\vec{0}$ is a vector of zeros). $B$ is formatted similarly to $C$ above, but contains a pattern of zeros, ones, and negative ones that specify how to take differences. It's constructed such that we have the following system of inequalities. Left of the peak: $p_1-p_2 \le 0, \ p_2-p_3 \le 0, \dots$. And right of the peak: $p_{152}-p_{151} \le 0, \ p_{151}-p_{150} \le 0, \dots$
Probability decreases to zero at 0 or 151 seats. This is simply a pair of constraints: $p_1 = 0$ and $p_{152} = 0$, which are incorporated into the system $C p = v$.
Probabilities vary slowly as a function of the number of seats, i.e. the distribution is 'smooth' (speaking loosely, since it's discrete). This assumption is imposed by constraining the squared second differences between the probabilities assigned to adjacent numbers of seats. This constraint is represented by the nonlinear inequality $g(p) \le \alpha$, where:
$$g(p) = \sum_{i=2}^{151} \big[ (p_{i+1}-p_i) - (p_i-p_{i-1}) \big]^2$$
$\alpha$ is a hyperparameter that controls smoothness; smaller values give smoother solutions. I set it to $2 \times 10^{-4}$. If set too low, it can contradict the other constraints, making a solution impossible.
Here's the result of solving the same MaxEnt problem as above (now with the additional constraints):
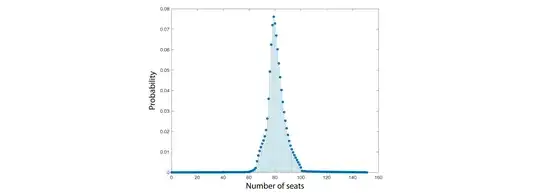
Clearly, the distribution is smoother. And, although it's hard to see in the plot, the tails taper monotonically to zero rather than remaining flat. I want to emphasize again that this is a consequence of particular assumptions rather than information specified in the problem itself. It's only reasonable to believe the result if the assumptions accurately embody prior knowledge learned from other problems.

