Not a duplicate since the linked question does not answer this question: A measure of similarity should be maximal for instances which are the same (e.g. similarity between (1,1) and (1,1) should be higher than the similarity between (1, 1) and (1, 2) ). This is not the case. Therefore the dot product is not a measure of similarity. Where am I wrong?
All explanations of the kernel trick I read take for granted that the dot product is a good measure of similarity for instances. I know that the dot product is zero if the vectors are orthogonal.
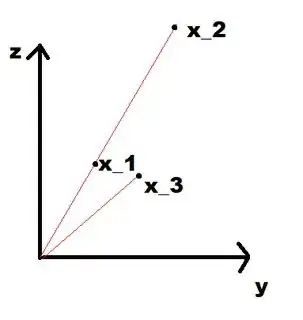
However, in this image, from my intuitive understanding $x_1$ and $x_3$ are quite similar, while $x_1$ and $x_2$ are very different. Yet, the dot product between $x_1$ and $x_2$ is large, and between $x_1$ and $x_3$ is smaller.
Take for example $x_1 = (1, 1)^T$, $x_2 = (20, 20)^T$, $x_3 = (1, 0.9)^T$. In what sense are $x_1$ and $x_2$ more similiar than $x_1$ and $x_3$? Why does the angle matter so much in practise?