For what values of $\beta \in \mathbb{R}$ is $t(x-x')=-||x-x'||^\beta$ a kernel?
I know that kernels of type $t(x-x')$ where $t$ is function that inverts the dissimilarity $x-x'$ into a similarity measure proportional to the kernel. In this case, by means of adding a negative sign in front.
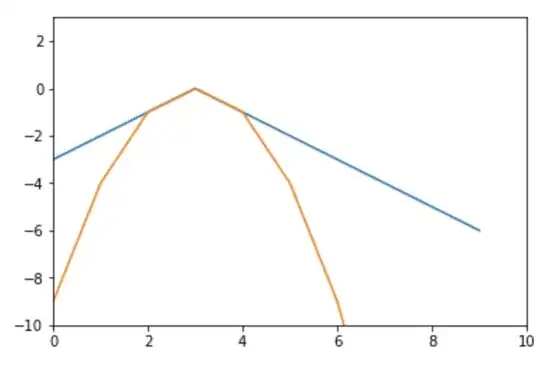
I have tried to plot several cases via Python and I observed that with $\beta>0$ I have sort of "concave" function, if you could call it like that:
With $\beta=0$ it is constant -1, and with $\beta<0$ I obtain a "convex" function with a division by zero at the origin. But with all that I do not answer to the question because I see plots, but I do not know how prove by which values of $\beta$ $t$ is a valid kernel. I would really appreciate your help!