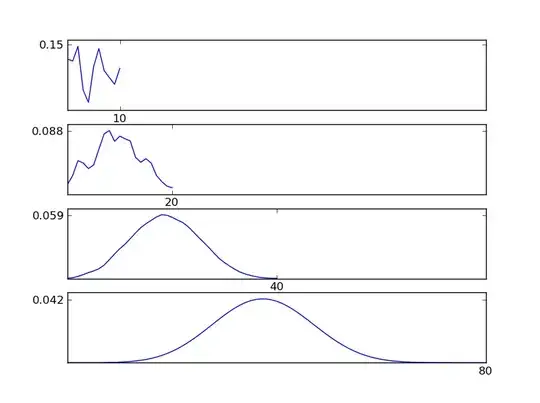
I am collecting averages of scores between 1 and 5 on a customer satisfaction survey. Sample sizes are routinely less than 20 for shorter periods. (Over longer periods, this is not a problem, as the sample size increases sufficiently.)
The population mean is expected at 4.78, and the population standard deviation is estimated to be .6.
I would have loved to use a t-table with n-1 degrees of freedom to get the confidence interval for two or three standard deviations for the sampling distribution. Unfortunately, with a sample size of 20, both two and three standard deviations to the right extend beyond the range of possible scores, meaning that sample size isn't even approximately normally distributed, right?
I am more interested in the spread of the data to the left, but I don't want this to be thrown off from the spread of the data to the right.
How can I get the probability of scoring a certain amount below or above the mean in such a situation with such a sample size?