3

i'm trying to solve this statistics problem.

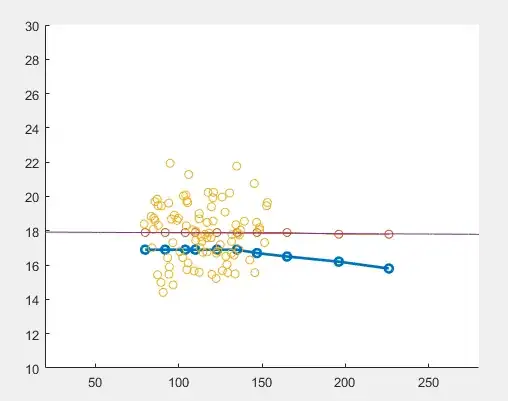
enter image description here

i have a certain number of samples that are randomly chosen to represent a population. (yellow dots in the picture)

over those samples are run tests to evaluate their "volume" and "water content".

let's say that the samples can be split in various classes of "volume" and that, for each of them, we infere the average "water content" (red dots in the picture) through a linear regression. (purple line in the picture)

we now want to calculate a "threshold value" for the "water content" into each class of "volume". this "theshold value" is defined as "water content" the that will ensure that 70% of our population in that class is above it. (blu dots in the picture. i have them but these will be needed to be calculated by my software in the future).

how can i do it?

here's my tests:

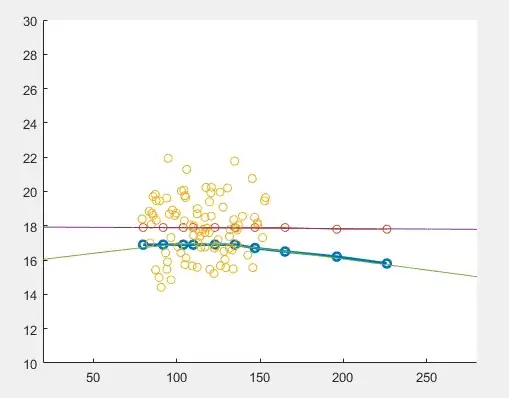
  1. i started by translating down the the linear regression curve by $0.53σ$ (where $σ$ is calculated over the samples' "water content"), but this curve is not the right answer to the problem (in matches some points, but not all due to a non-linear error).

enter image description here

  1. i calculated the lower bound of the confidence interval for the linear regression with $alpha=0.4$, but neither this curve is the right answer to the problem (it seems to follow the non-linear behavior of the threshold curve, but it's translated).

enter image description here

  1. i combined the two previous tests and i subtracted $0.4σ$ (because it made the curve seemd to fit the threshold points i had) to the lower bound of the confidence interval, and it seemd to work. but i can't really understand why this works.

enter image description here

what is the right way to do this calculation?

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
dmtg
  • 31
  • 1
  • How important is it to get the 70th percentile rather than the 69th or 71st (or 65th vs 75th)? Is it worse to miss high than to miss low? – Dave Sep 12 '19 at 17:56
  • thank you all for your answers and for the extremely valuable discussion. i spent some hours studying before answering back. i don't have a precise answer to this question, what i do know is that 70% of the population has to have a "water content" result above a certain value (let's call it the "minimum value for acceptance", MVFA) for each class of "volume". for this reason we calculate this "threshold value" that indicates that 70% of population is above it and we confront it with the MVFA. if our threshold is above the MVFA goods are ok for that class of "volume", if not, they are rejected. – dmtg Sep 13 '19 at 08:31
  • Okay, then this does sound like quantile regression. Listen to Stephan Kolassa. – Dave Sep 13 '19 at 08:48

1 Answers1

6

This is a straightforward case of quantile regression for a 30% quantile. This will fit a 30% quantile response, i.e., the response will exceed 30% of your population at the specified covariate value, so 70% will be above it. Your predictors can enter linearly, or you can do anything you can do with "standard" OLS, such as interactions or polynomial transformations.

We have a tag, and I recommend Roger Koenker's textbook Quantile Regression. Your software may support quantile regression, e.g., the quantreg package for R.

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
  • 1
    My first thought was quantile regression, but requiring something like "ensure it's greater than 70% of the population" makes me think that there should be a "normal" penalty for missing low and a very high penalty for missing high, so if quantile 0.70 is 1, predicting 0.9 results in a penalty of 0.1 while predicting 1.1 results in a penalty of 10! (That's a factorial.) Perhaps I'm thinking of something like a very asymmetric confidence interval about the estimated value. – Dave Sep 12 '19 at 11:56
  • 2
    @Dave: I think your intuition with an asymmetric loss function is very close to the hinge loss that is used in quantile regression. – Stephan Kolassa Sep 12 '19 at 13:10
  • 2
    @Dave see https://stats.stackexchange.com/questions/251600 for a derivation of the loss function in quantile regression. – whuber Sep 12 '19 at 13:13
  • i'm trying to implement your precious suggestions into my script and i'll be back soon to show my progress. – dmtg Sep 13 '19 at 08:40