1

Pdf of a distribution is shown in the figure below. Is there a way to estimate the first tail (or) to segment first mode and its tail?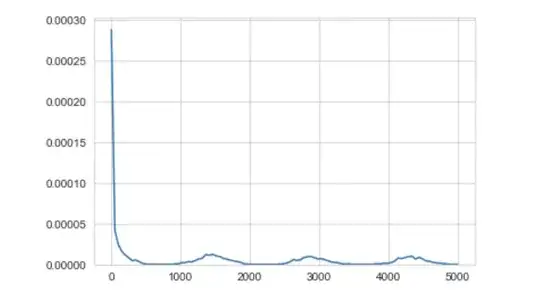enter image description here

he KDE plot resulted from a transaction dataset where transactions occur at two frequencies - one immediately after and the other after a while. Hence the first peak. My goal is to identify transactions happening immediately after. By visualization, I found that 600 would be an optimum value for this distribution but is there any statistical way to determine this?

Edit: My goal is to segment the sub-population corresponding to the big peak around zero from the rest.

Augustine Samuel
  • 19
  • 5
  • I’m not sure that this happened to you, but KDE plots with extreme values can give misleading ideas about peaks way far out. Those three apparent peaks may not really be there. – Dave Sep 06 '19 at 10:55
  • Could you explain what a "first tail" of a distribution might be? – whuber Sep 06 '19 at 13:51
  • @whuber Where the peak ends and next mode begins – Augustine Samuel Sep 06 '19 at 17:47
  • Which peak? I see at least ten of them. – whuber Sep 06 '19 at 17:50
  • @whuber The tail between 0 and 1000 – Augustine Samuel Sep 06 '19 at 17:56
  • 1
    That's not a "tail:" it's just part of the distribution. As suggested by @Dave, what's happening between $0$ and $1000$ depends as much or more on the kernel and bandwidth you are using as it does not the data, making it difficult to conceive of any sense in which one might "estimate" the behavior in this region. – whuber Sep 06 '19 at 20:18
  • @whuber There are four kind of obvious peaks. Let's say these correspond to four sub-populations. What would you think of saying something about the sub-population corresponding to the big peak around zero? I think that's more along the lines of what was meant. – Dave Sep 09 '19 at 13:04
  • @Dave Thank you. I can also conceive of other interpretations, such as asking about the right tail rather than the left. That's why this question needs clarification from the OP, not from us. – whuber Sep 09 '19 at 13:25
  • @Dave Thank you. That is exactly what I wanted. I've edited the question. – Augustine Samuel Sep 10 '19 at 05:55

0 Answers0