I have read this Confusion around Bellman (update) operator and yet I am not clear about the difference between the two equations $V^{\pi }(s)=R(s,\pi (s))+\gamma \sum _{s'}P(s'|s,\pi (s))V^{\pi }(s').\ $ from https://en.wikipedia.org/wiki/Bellman_equation and 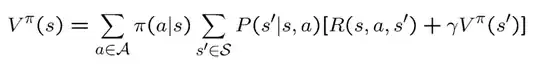
that I read from here https://www.cs.cmu.edu/~mgormley/courses/10601-s17/slides/lecture26-ri.pdf and many other places. All helps and clarifications are welcome and will be very helpful. Thank you.