How to determine whether a validation study produces acceptable results?

Question

I have a method developed to predict results of a signal that outputs an root mean squared error (RMSE) for each subject. Combining all 40 subjects (2 samples for each subject), I get a mean RMSE of 5.5 with a standard deviation of 2.8. This is comparable to previous literature.

Now I did a validation study using 5 subjects (2 samples each) and obtained a mean RMSE of 12.4 with a standard deviation of 4.4.

To me these seem drastically different and I would not be able to conclude that the validation is good, but I want a more quantitative way to describe that. How would I go about this? I also feel like the 5 subjects is not a suitable sample size, so how would I determine an adequate sample size for the validation study?

My intra-ocular trauma test looks like this:

Answer 1

The classical way of testing whether two (R)MSEs would be the Diebold-Mariano test. However, this is an asymptotic test, and you have a rather small sample size, so something else would be in order.

Let's simulate some data. I'll use R.

set.seed(1)
group_1 <- rnorm(40,mean=5.5,sd=2.8)
group_2 <- rnorm(5,mean=12.4,sd=4.4)

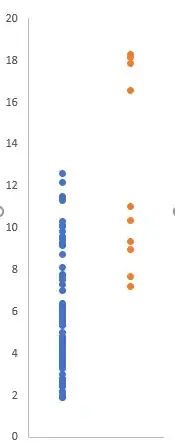
Now, the first test to run is the so-called intra-ocular trauma test. The name derives from the fact that if you simply plot your data, the effect might hit you right between the eyes. Or not. With our simulated data, it does:

plot(rep(1,length(group_1)),group_1,xlim=c(.8,2.2),ylim=range(c(group_1,group_2)),
    pch=19,xlab="",ylab="RMSE",xaxt="n",las=2)
points(rep(2,length(group_2)),group_2,pch=19)
axis(1,at=1:2,labels=c("Group 1","Group 2"))

In case this does not work for your actual data, or is not quite as obvious as here, I would recommend a permutation test. The null hypothesis is that the two groups come from the same population, and our test statistic will be the difference in mean RMSEs. We can simulate the distribution of this test statistic under the null hypothesis by randomly permuting the group labels on our RMSEs and calculating the differences in means. Let's do so and see where in this simulated null distribution the actually observed difference in means lies:

n_perms <- 1e4
means_perms <- rep(NA,n_perms)
for ( ii in 1:n_perms ) {
    index <- sample(x=seq_along(c(group_1,group_2)),size=length(group_2),replace=FALSE)
    means_perms[ii] <- mean(c(group_1,group_2)[index])-mean(c(group_1,group_2)[-index])
}
mean_actual <- mean(group_2)-mean(group_1)

1-ecdf(means_perms)(mean_actual)
hist(means_perms,col="grey",xlim=range(c(mean_actual,means_perms)))
abline(v=mean_actual,lwd=2,col="red")

It turns out that not a single one of the 10,000 permuted means differences is larger than the one we actually observed, so in this case, we can reject the null hypothesis with $p<.0001$. This kind of permutation test is a very basic one and is treated in most permutation testing textbooks.

If you want to determine a sample size that will allow you to detect a given effect size, you could simply calculate Cohen's $d$ and use any number of online power calculators. These again are asymptotic, but if your sample size hits about 20, they should be good enough.