Here is a result in R, using the auto.arima function in the forecast package. auto.arima automatically determines the necessary AR, MA, d, S components and also allows you to include other variables.
> library(readxl)
> A=read_excel("A.xlsx")
> B=read_excel("B.xlsx")
> A1=ts(A$Value,frequency=4)
> B1=ts(B$Value,frequency=4)
> library(forecast)
> mod=auto.arima(A1,xreg=B1,stepwise=F,approximation=F)
> summary(mod)
Series: A1
Regression with ARIMA(0,1,0) errors
Coefficients:
xreg
0.4091
s.e. 0.1570
sigma^2 estimated as 0.002247: log likelihood=126.03
AIC=-248.06 AICc=-247.89 BIC=-243.37
Training set error measures:
ME RMSE MAE MPE MAPE
Training set -0.001337502 0.04678851 0.03242543 -0.3753579 5.792672
MASE ACF1
Training set 0.4114466 0.08525872
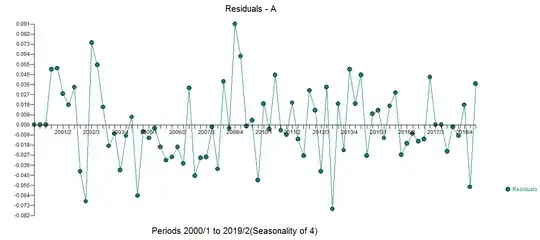
So the selected model contains only 1 term, the lag of B. Check the residuals:
> checkresiduals(mod)
Ljung-Box test
data: Residuals from Regression with ARIMA(0,1,0) errors
Q* = 7.354, df = 7, p-value = 0.393
Model df: 1. Total lags used: 8
Look OK. Let's try a model without B:
> mod=auto.arima(A1,stepwise=F,approximation=F)
> summary(mod)
Series: A1
ARIMA(1,1,0)
Coefficients:
ar1
0.1743
s.e. 0.1114
sigma^2 estimated as 0.002369: log likelihood=123.98
AIC=-243.95 AICc=-243.79 BIC=-239.26
Training set error measures:
ME RMSE MAE MPE MAPE MASE
Training set -0.001066886 0.04804238 0.03242514 -0.55368 5.841148 0.4114429
ACF1
Training set -0.01470753
> checkresiduals(mod)
Ljung-Box test
data: Residuals from ARIMA(1,1,0)
Q* = 4.033, df = 7, p-value = 0.776
Model df: 1. Total lags used: 8
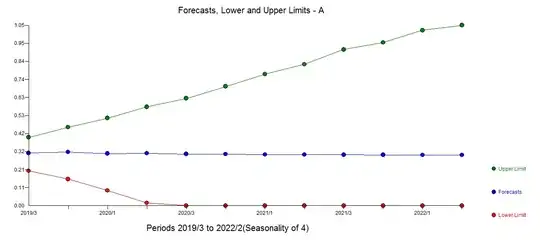
This model is very similar to the previous in terms of accuracy, and includes only 1 AR term, suggesting that you may as well forecast based on A alone.