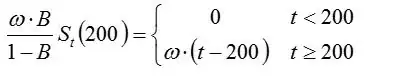2

enter image description here

I'm facing an issue with understanding what the normalisation process means and how its used.

I've been given a probability density function, and the information that a value of C=1/a 'normalises this function'.

Using this information, I am to determine the mean and variance of the given random variable, x.

Searching online for an answer only confused me more because there seem to be different formulae being used to characterise the normalisation process.

Ferdi
  • 4,882
  • 7
  • 42
  • 62
fastingfeasting
  • 77
  • 3
  • 3
    Normalisation can have many different meanings. Even in probability, it can have multiple meanings. Of course it means something like "changing the variables so that things become easier to calculate or that they conform to a norm". One type of normalisation is when you want to change the variable that has a normal distribution, so that it fits to the **standard** normal, $N(0,1)$. Alternatively, it can mean that we want the integral of the PDF over the support to be equal to $1$. So, without any context, it's difficult to say ... –  Aug 29 '19 at 10:19
  • @MattiP. Thanks so much for replying. I've been able to edit my question with a screenshot of the problem. You've kind of touched on both of the definitions I came across when searching for guidance. Here, I'm unsure what approach I need to take, because while it seems easy to use the integral over the PDF method which the question pushes us towards, but what does it mean to change the variable so that it fits N(0,1)? Again, thanks so much for replying, I really appreciate it. –  Aug 29 '19 at 10:51
  • Okay it seems like the normalisation is exactly about the integral being equal to one. In this case, the normal distribution things do not apply because the variable in case is not normally distributed. In fact, it has the PDF given in the problem statement. –  Aug 29 '19 at 11:00
  • 2
    Onto the actual problem: You are given the probability density function and actually, if you read carefully, the normalisation has already been carried out. Now you only need to find the expected value and variance of the random variable. Do you think you can do it? –  Aug 29 '19 at 11:03
  • @MattiP. I think I understand now. If I integrate a^-2 and multiply that to the integral already provided, I can find out a value for a, which will simplify the original PDF. Or do I integrate 1/C as log(C) and then turn that into log (1/a^2)? Thanks for helping me through this! EDIT: Integrating a^-2 as -1/x led me to a=-1, which makes the original PDF equal x*(e^x), which looks wrong. –  Aug 29 '19 at 11:39
  • 1
    You need not worry about $a$ or $C$, because they have already been computed. It was given that $$ C= \frac{1}{a^2} $$ And plugging this in, the PDF of the random variable is $$ f(x) = a^2 x e^{-ax}\qquad, x\geq 0 $$ You see how this has a parameter $a$ ? Consider it "some value that will be plugged in later". So now you need to find the expected value of the variable. Do you know how to calculate the expected value of a random variable, given its PDF? –  Aug 29 '19 at 11:43
  • @MattiP. Okay, I arrived at that PDF as well. Here, when I now integrate this PDF and set it to 1, would I treat a^2 as a constant or a variable? And no, I'm not familiar with that right now, so I'm looking that up now! –  Aug 29 '19 at 12:26
  • 1
    All the work has been done for you at https://stats.stackexchange.com/questions/198595/expected-value-of-gamma-distribution/198621#198621. You only need to apply those results to solve for $a.$ – whuber Aug 29 '19 at 12:43
  • 1
    Self-study questions need to be so indicated. https://stats.stackexchange.com/tags/self-study/info – Carl Aug 30 '19 at 01:42

1 Answers1

2

The normalising here means that the constant C will make the function $f(x)$ a proper probability density function, which in this case means the integration of $f(x)$ from 0 to infinity equals to 1, because $f(x)$ only spans the $[0,\infty)$ interval, which is commonly referred to as semi-infinite support.

Carl
  • 11,532
  • 7
  • 45
  • 102
Yunlong Huang
  • 36
  • 1