Suppose I have a continuous random variable which is bound between 0 and 1. The distribution is left skewed like the picture below:
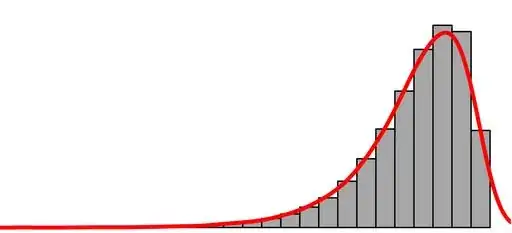
My goal is to identify outliers that are small or farther away from 1. In other words, I don't care about outliers that exist on the right side.
In an attempt to perform outlier detection, I decided that I could represent the data with a Beta distribution and use scipy to estimate the parameters of that distribution. Then, I computed the CDF and then chose a probability of observing a value as great as X_c, P(X_c>x), such that every point, x, below X_c is anomalous.
Does this approach seem reasonable? I could not find any resources on using a beta distribution to model data unless it was being used as a prior for bayesian updating. The distribution seems appropriate to me for my use case due to its ability to model the shape of the data I am dealing with and because it is a valid probability distribution.