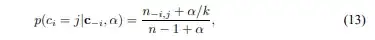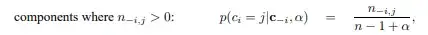For the Chinese restaurant process, as used in Dirichlet Process mixture models, we have a prior that data point i belongs to cluster j, where c is an indicator. n represents the total number of data points that are assigned to cluster j, where subscript -i refers to all observations excpet i.
As we take k to infinity, (which represents taking the number of components in the mixture model to infinity), the expression transforms to
when that cluster already exists (which I understand).
For the case that the cluster doesn't already exist, the prior transforms to
This is where my problem lies - how does alpha feature in this expression if (alpha/k) tends to 0 as k tends to infinity?
Thanks in advance
edit: link to paper (pages 3-4) https://www.seas.harvard.edu/courses/cs281/papers/rasmussen-1999a.pdf