What exactly are keys, queries, and values in attention mechanisms?

Question

How should one understand the keys, queries, and values that are often mentioned in attention mechanisms?

I've tried searching online, but all the resources I find only speak of them as if the reader already knows what they are.

Judging by the paper written by Bahdanau (Neural Machine Translation by Jointly Learning to Align and Translate), it seems as though values are the annotation vector $h$ but it's not clear as to what is meant by "query" and "key."

The paper that I mentioned states that attention is calculated by

$$c_i = \sum^{T_x}_{j = 1} \alpha_{ij} h_j$$

with

$$ \begin{align} \alpha_{ij} & = \frac{e^{e_{ij}}}{\sum^{T_x}_{k = 1} e^{ik}} \\\\ e_{ij} & = a(s_{i - 1}, h_j) \end{align} $$

Where are people getting the key, query, and value from these equations?

Thank you.

Answer 1

The key/value/query formulation of attention is from the paper Attention Is All You Need.

How should one understand the queries, keys, and values

The key/value/query concept is analogous to retrieval systems. For example, when you search for videos on Youtube, the search engine will map your query (text in the search bar) against a set of keys (video title, description, etc.) associated with candidate videos in their database, then present you the best matched videos (values).

The attention operation can be thought of as a retrieval process as well.

As mentioned in the paper you referenced (Neural Machine Translation by Jointly Learning to Align and Translate), attention by definition is just a weighted average of values,

$$c=\sum_{j}\alpha_jh_j$$ where $\sum \alpha_j=1$.

If we restrict $\alpha$ to be a one-hot vector, this operation becomes the same as retrieving from a set of elements $h$ with index $\alpha$. With the restriction removed, the attention operation can be thought of as doing "proportional retrieval" according to the probability vector $\alpha$.

It should be clear that $h$ in this context is the value. The difference between the two papers lies in how the probability vector $\alpha$ is calculated. The first paper (Bahdanau et al. 2015) computes the score through a neural network $$e_{ij}=a(s_i,h_j), \qquad \alpha_{i,j}=\frac{\exp(e_{ij})}{\sum_k\exp(e_{ik})}$$ where $h_j$ is from the encoder sequence, and $s_i$ is from the decoder sequence. One problem of this approach is, say the encoder sequence is of length $m$ and the decoding sequence is of length $n$, we have to go through the network $m*n$ times to acquire all the attention scores $e_{ij}$.

A more efficient model would be to first project $s$ and $h$ onto a common space, then choose a similarity measure (e.g. dot product) as the attention score, like $$e_{ij}=f(s_i)g(h_j)^T$$ so we only have to compute $g(h_j)$ $m$ times and $f(s_i)$ $n$ times to get the projection vectors and $e_{ij}$ can be computed efficiently by matrix multiplication.

This is essentially the approach proposed by the second paper (Vaswani et al. 2017), where the two projection vectors are called query (for decoder) and key (for encoder), which is well aligned with the concepts in retrieval systems. (There are later techniques to further reduce the computational complexity, for example Reformer, Linformer.)

How are the queries, keys, and values obtained

The proposed multihead attention alone doesn't say much about how the queries, keys, and values are obtained, they can come from different sources depending on the application scenario.

$$ \begin{align}\text{MultiHead($Q$, $K$, $V$)} & = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^{O} \\ \text{where head$_i$} & = \text{Attention($QW_i^Q$, $KW_i^K$, $VW_i^V$)} \end{align}$$ Where the projections are parameter matrices: $$ \begin{align} W_i^Q & \in \mathbb{R}^{d_\text{model} \times d_k}, \\ W_i^K & \in \mathbb{R}^{d_\text{model} \times d_k}, \\ W_i^V & \in \mathbb{R}^{d_\text{model} \times d_v}, \\ W_i^O & \in \mathbb{R}^{hd_v \times d_{\text{model}}}. \end{align}$$

For unsupervised language model training like GPT, $Q, K, V$ are usually from the same source, so such operation is also called self-attention.

For the machine translation task in the second paper, it first applies self-attention separately to source and target sequences, then on top of that it applies another attention where $Q$ is from the target sequence and $K, V$ are from the source sequence.

For recommendation systems, $Q$ can be from the target items, $K, V$ can be from the user profile and history.

Answer 2

I was also puzzled by the keys, queries, and values in the attention mechanisms for a while. After searching on the Web and digesting relevant information, I have a clear picture about how the keys, queries, and values work and why they would work!

Let's see how they work, followed by why they work.

In a seq2seq model, we encode the input sequence to a context vector, and then feed this context vector to the decoder to yield expected good output.

However, if the input sequence is long, relying on only one context vector become less effective. We need all the information from the hidden states in the input sequence (encoder) for better decoding (the attention mechanism).

One way to utilize the input hidden states is shown below: Image source: https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3

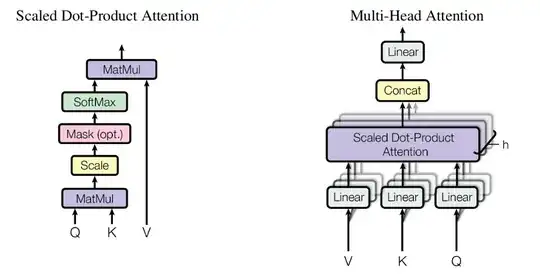
In other words, in this attention mechanism, the context vector is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key (this is a slightly modified sentence from [Attention Is All You Need] https://arxiv.org/pdf/1706.03762.pdf).

Here, the query is from the decoder hidden state, the key and value are from the encoder hidden states (key and value are the same in this figure). The score is the compatibility between the query and key, which can be a dot product between the query and key (or other form of compatibility). The scores then go through the softmax function to yield a set of weights whose sum equals 1. Each weight multiplies its corresponding values to yield the context vector which utilizes all the input hidden states.

Note that if we manually set the weight of the last input to 1 and all its precedences to 0s, we reduce the attention mechanism to the original seq2seq context vector mechanism. That is, there is no attention to the earlier input encoder states.

Now, let's consider the self-attention mechanism as shown in the figure below:

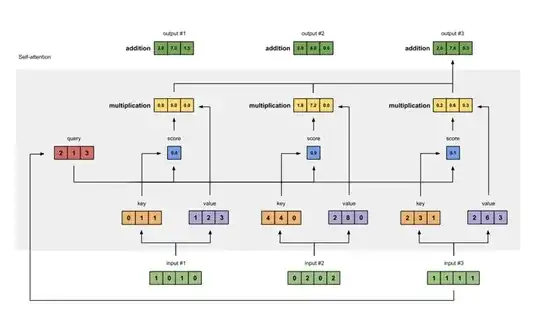Image source: https://towardsdatascience.com/illustrated-self-attention-2d627e33b20a

The difference from the above figure is that the queries, keys, and values are transformations of the corresponding input state vectors. The others remain the same.

Note that we could still use the original encoder state vectors as the queries, keys, and values. So, why we need the transformation? The transformation is simply a matrix multiplication like this:

Query = I x W(Q)

Key = I x W(K)

Value = I x W(V)

where I is the input (encoder) state vector, and W(Q), W(K), and W(V) are the corresponding matrices to transform the I vector into the Query, Key, Value vectors.

What are the benefits of this matrix multiplication (vector transformation)?

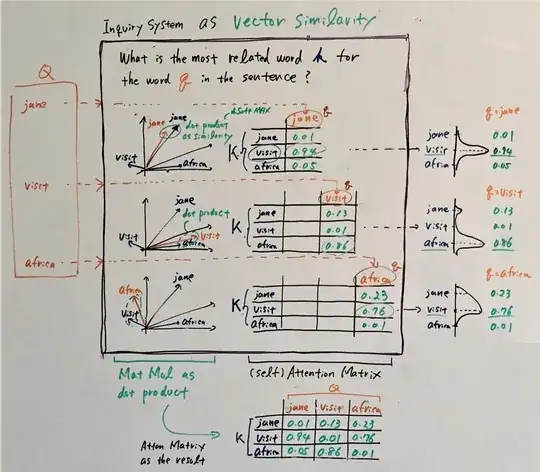
The obvious reason is that if we do not transform the input vectors, the dot product for computing the weight for each input's value will always yield a maximum weight score for the individual input token itself. This may not be the desired case, say, for the pronoun token that we need it to attend to its referent.

Another less obvious but important reason is that the transformation may yield better representations for Query, Key, and Value. Recall the effect of Singular Value Decomposition (SVD) like that in the following figure:

Image source: https://youtu.be/K38wVcdNuFc?t=10

By multiplying an input vector with a matrix V (from the SVD), we obtain a better representation for computing the compatibility between two vectors, if these two vectors are similar in the topic space as shown in the example in the figure.

And these matrices for transformation can be learned in a neural network!

In short, by multiplying the input vector with a matrix, we got:

1. increase of the possibility for each input token to attend to other tokens in the input sequence, instead of individual token itself.

2. possibly better (latent) representations of the input vector;

3. conversion of the input vector into a space with a desired dimension, say, from dimension 5 to 2, or from n to m, etc (which is practically useful);

Note the transformation matrix is learnable (without manual setting).

I hope this help you understand the queries, keys, and values in the (self-)attention mechanism of deep neural networks.

Answer 3

See Attention is all you need - masterclass, from 15:46 onwards Lukasz Kaiser explains what q, K and V are.

So basically:

• q = the vector representing a word
• K and V = your memory, thus all the words that have been generated before. Note that K and V can be the same (but don't have to).

So what you do with attention is that you take your current query (word in most cases) and look in your memory for similar keys. To come up with a distribution of relevant words, the softmax function is then used.

Answer 4

Tensorflow and Keras just expanded on their documentation for the Attention and AdditiveAttention layers. Here is a sneaky peek from the docs:

The meaning of query, value and key depend on the application. In the case of text similarity, for example, query is the sequence embeddings of the first piece of text and value is the sequence embeddings of the second piece of text. key is usually the same tensor as value.

But for my own explanation, different attention layers try to accomplish the same task with mapping a function $f: \Bbb{R}^{T\times D} \mapsto \Bbb{R}^{T \times D}$ where T is the hidden sequence length and D is the feature vector size. For the case of global self- attention which is the most common application, you first need sequence data in the shape of $B\times T \times D$, where $B$ is the batch size. Each forward propagation (particularly after an encoder such as a Bi-LSTM, GRU or LSTM layer with return_state and return_sequences=True for TF), it tries to map the selected hidden state (Query) to the most similar other hidden states (Keys). After repeating it for each hidden state, and softmax the results, multiply with the keys again (which are also the values) to get the vector that indicates how much attention you should give for each hidden state. I hope this helps anyone as it took me days to figure it out.

Answer 5

I'm going to try provide an English text example. The following is based solely on my intuitive understanding of the paper 'Attention is all you need'.

Say you have a sentence:

• I like Natural Language Processing , a lot !

Assume that we already have input word vectors for all the 9 tokens in the previous sentence. So, 9 input word vectors.

Looking at the encoder from the paper 'Attention is all you need', the encoder needs to produce 9 output vectors for each word. This is done, through the Scaled Dot-Product Attention mechanism, coupled with the Multi-Head Attention mechanism. I'm going to focus only on an intuitive understanding of the Scaled Dot-Product Attention mechanism, and I'm not going to go into the scaling mechanism.

Walking through an example for the first word 'I':

• The query is the input word vector for the token "I"

• The keys are the input word vectors for all the other tokens, and for the query token too, i.e (semi-colon delimited in the list below):

  [like;Natural;Language;Processing;,;a;lot;!] + [I]

• The word vector of the query is then DotProduct-ed with the word vectors of each of the keys, to get 9 scalars / numbers a.k.a "weights"

• These weights are then scaled, but this is not important to understand the intuition

• The weights then go through a 'softmax' which is a particular way of normalizing the 9 weights to values between 0 and 1. This becomes important to get a "weighted-average" of the value vectors , which we see in the next step.

• Finally, the initial 9 input word vectors a.k.a values are summed in a "weighted average", with the normalized weights of the previous step. This final step results in a single output word vector representation of the word "I"

Now that we have the process for the word "I", rinse and repeat to get word vectors for the remaining 8 tokens. We now have 9 output word vectors, each put through the Scaled Dot-Product attention mechanism. You can then add a new attention layer/mechanism to the encoder, by taking these 9 new outputs (a.k.a "hidden vectors"), and considering these as inputs to the new attention layer, which outputs 9 new word vectors of its own. And so on ad infinitum.

If this Scaled Dot-Product Attention layer summarizable, I would summarize it by pointing out that each token (query) is free to take as much information using the dot-product mechanism from the other words (values), and it can pay as much or as little attention to the other words as it likes by weighting the other words with (keys) . The real power of the attention layer / transformer comes from the fact that each token is looking at all the other tokens at the same time (unlike an RNN / LSTM which is restricted to looking at the tokens to the left)

The Multi-head Attention mechanism in my understanding is this same process happening independently in parallel a given number of times (i.e number of heads), and then the result of each parallel process is combined and processed later on using math. I didn't fully understand the rationale of having the same thing done multiple times in parallel before combining, but i wonder if its something to do with, as the authors might mention, the fact that each parallel process takes place in a separate Linear Algebraic 'space' so combining the results from multiple 'spaces' might be a good and robust thing (though the math to prove that is way beyond my understanding...)

Answer 6

Where are people getting the key, query, and value from these equations?

The paper you refer to does not use such terminology as "key", "query", or "value", so it is not clear what you mean in here. There is no single definition of "attention" for neural networks, so my guess is that you confused two definitions from different papers.

In the paper, the attention module has weights $\alpha$ and the values to be weighted $h$, where the weights are derived from the recurrent neural network outputs, as described by the equations you quoted, and on the figure from the paper reproduced below.

Similar thing happens in the Transformer model from the Attention is all you need paper by Vaswani et al, where they do use "keys", "querys", and "values" ($Q$, $K$, $V$). Vaswani et al define the attention cell differently:

$$ \mathrm{Attention}(Q, K, V) = \mathrm{softmax}\Big(\frac{QK^T}{\sqrt{d_k}}\Big)V $$

What they also use is multi-head attention, where instead of a single value for each $Q$, $K$, $V$, they provide multiple such values.

Where in the Transformer model, the $Q$, $K$, $V$ values can either come from the same inputs in the encoder (bottom part of the figure below), or from different sources in the decoder (upper right part of the figure). This part is crucial for using this model in translation tasks.

In both papers, as described, the values that come as input to the attention layers are calculated from the outputs of the preceding layers of the network. Both paper define different ways of obtaining those values, since they use different definition of attention layer.

Answer 7

Forget about V

Focus on what the objective of MatMul is in the Scaled dot product attention using Q and K.

Attention

For the sentence "jane visits africa".

When your eyes see jane, your brain looks for the most related word in the rest of the sentence to understand what jane is about (query). Your brain focuses or attends to the word visit (key).

This process happens for each word in the sentence as your eyes progress through the sentence.

Inquiry System as Vector Similarity

The MatMul implements an inquiry system or question-answer system that imitates this bran function, as a Vector Similarity Calculation.

The system process the inquiry:

For the word q that your eyes see in the given sentence, what is the most related word k in the sentence to understand what q is about?

and provides the answer as the probability.

q	k	probability
jane	visit	0.94
visit	africa	0.86
africa	visit	0.76

Note that the softmax to normalize the probability (in green) has been implicitly incorporated in the diagram.

There are multiple ways to calculate the similarity between vectors such as cosine similarity. Transformer attention uses simple dot product.

Where are Q and K are from

The transformer encoder training builds the weight parameter matrices WQ and Wk in the way Q and K builds the Inquiry System that answers the inquiry "What is k for the word q".

References

There are multiple concepts that will help understand how the self attention in transformer works, e.g. embedding to group similars in a vector space, data retrieval to answer query Q using the neural network and vector similarity.

• CS480/680 Lecture 19: Attention and Transformer Networks - This is probably the best explanation I found that actually explains the attention mechanism from the database perspective.
• Illustrated Guide to Transformers Neural Network: A step by step explanation
  
• Distributed Representations of Words and Phrases and their Compositionality - It helps understand how word2vec works to group/categorize words in a vector space by pulling similar words together, and pushing away non-similar words using negative sampling.
• Generalized End-to-End Loss for Speaker Verification - Continuation to understand embedding to pull together siimilars and pushing away non-similars in a vector space.
• Transformer model for language understanding - TensorFlow implementation of transformer
• The Annotated Transformer - PyTorch implementation of Transformer

Answer 8

• Queries is a set of vectors you want to calculate attention for.
• Keys is a set of vectors you want to calculate attention against.
• As a result of dot product multiplication you'll get set of weights a (also vectors) showing how attended each query against Keys. Then you multiply it by Values to get resulting set of vectors.

Now let's look at word processing from the article "Attention is all you need". There are two self-attending (xN times each) blocks, separately for inputs and outputs plus cross-attending block transmitting knowledge from inputs to outputs.

Each self-attending block gets just one set of vectors (embeddings added to positional values). In this case you are calculating attention for vectors against each other. So Q=K=V. You just need to calculate attention for each q in Q.

Cross-attending block transmits knowledge from inputs to outputs. In this case you get K=V from inputs and Q are received from outputs. I think it's pretty logical: you have database of knowledge you derive from the inputs and by asking Queries from the output you extract required knowledge.

How attention works: dot product between vectors gets bigger value when vectors are better aligned. Then you divide by some value (scale) to evade problem of small gradients and calculate softmax (when sum of weights=1). At this point you get set of weights sum=1 that tell you for which vectors in Keys your query is better aligned. All that's left is to multiply by Values.

Answer 9

This is more proper being a comment but I do not have enough reputation to comment. (Plz up vote for me if you find the following is useful. :))

What are K and V? Are they the same?

The short answer is that they can be the same, but technically they do not need to be the same.

Briefly introduce K, V, Q but highly recommend the previous answers: In the Attention is all you need paper, this Q, K, V are first introduced. In that paper, generally(which means not self attention), the Q is the decoder embedding vector(the side we want), K is the encoder embedding vector(the side we are given), V is also the encoder embedding vector. And this attention mechanism is all about trying to find the relationship(weights) between the Q with all those Ks, then we can use these weights(freshly computed for each Q) to compute a new vector using Vs(which should related with Ks). If this is self attention: Q, V, K can even come from the same side -- eg. compute the relationship among the features in the encoding side between each other.(Why not show strong relation between itself? Projection.)

Case where they are the same: here in the Attention is all you need paper, they are the same before projection. Also in this transformer code tutorial, V and K is also the same before projection.

Case where K and V is not the same: In the paper End-to-End Object Detection Appendix A.1 Single head(this part is an introduction for multi head attention, you do not have to read the paper to figure out what this is about), they offer an intro to multi-head attention that is used in the Attention is All You Need papar, here they add some positional info to the K but not to the V in equation (7), which makes the K and the V here are not the same.

Hope this helps.